在《数学》(必修1,普通高中课程标准实验教科书,人民教育出版社)中第三章第3.2节《函数模型及其应运》的第二节课时里安排的学习内容是“指数函数、对数函数和幂函数的增长速度”,课本中采用的方法是三类函数中各取一个在第一象限上的具体的增函数,采用合情推理和直观分析的方式得出三类增函数的增长不在同一个“档次”上的结论。
经过思考,我觉得这节内容是今后学习变化率和导数的很好素材,而教材上的处理停留在定性分析的层面,没有很好的发掘出承上启下的功能,所以想重新组建教学素材,构建出由定性到定量分析过程。
1.我选择的函数是:

选择的理由是:
1)、三类函数中,指数函数和对数函数各取了一个,他们互为反函数。而幂函数取了两个,他们也互为反函数。
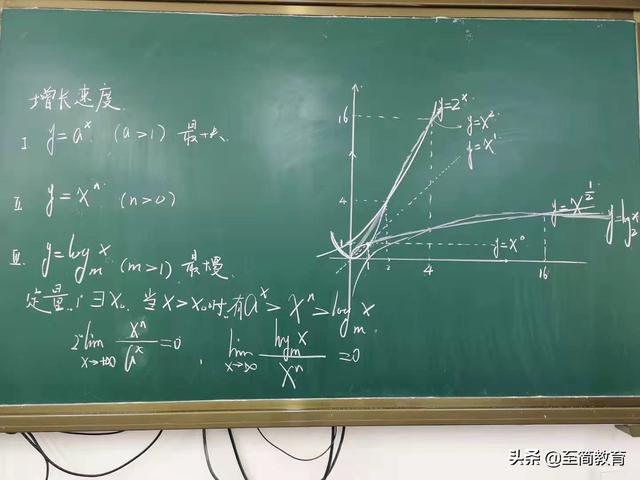
2)、看看他们的图像,注意它们的交点,这是学生非常容易出错的地方。

3)、可以看出当x的值大于4的时候,其增长率出现了明显的差距。
2.和课本相比,我增加了下列表格用来定量说明增长幅度,也想在这里为今后学习导数做了铺垫。

3.在知识总结上,从两个方面说明增长的“档次”不一样。
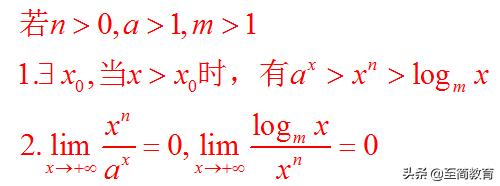
4.课堂板书

5.做一个温暖的教师,做有温度的教育。






