八省联考中的小学数学,作者:benqu
对于2021年参加高考的高三学生来说,备受关注的一次考试就是八省联考。这是针对2021年高考改革的八个省份,由教育部命制语文、数学、英语试题,以便考生熟悉改革后高考的题型和考察内容。最近,八个省份陆续公布了成绩,但数学成绩都不理想,江苏省平均分也只有69分,其他省份平均分在52分左右。
学生的平均分为何不佳?如何使他们提高成绩?我作为一名熟悉小考、中考、高考、考研等国内外数学考试的“题库”,早已料到中国学生存在的薄弱点。其中一个原因,是和小学教学相关。这次考试很多题目都是以小学数学和简单的数学知识作为背景的,很多学生小学数学基础不扎实,到了中学后,只会题海战术刷高考题,而有些小学数学的思维和方法,他们没有建立起来,也没有学过相应的教材或讲义。因此,他们漏洞在“八省联考”暴露出来。
下面我举例几题说明。“八省联考”一共22道题,以下几个题目,仅仅通过小学知识就可以解答。这反映了目前高考的命题趋势:难度较低,对数学思维和基础素养有一定的考察。

无论是小学生学数学还是学编程,首先都打下最基础的离散数学知识,其中第一个知识点就是逻辑和集合,最基本的智能思维。什么是集合?把几个事物放在一个容器就是集合。{赵,钱,孙,李}是一个集合,{1,2,3,4}也是一个集合。
小学生没有学过集合的运算和符号(交集、并集、补集、包含),但用几句话举例就可以教给他们了。设集合的全集R={1,2,3,4},设M={1,2},则M的补集就是{3,4}。M包含于N,可以设N={2,3,4}。
再看题目求解的式子,N的补集是{1},M与它的并集就是{1,2},就是M。

这是小学数学应该掌握的最基本的排列组合知识。学生通过穷举法就可以解答。如果小学生不会解答,他的难点在于不会将文字叙述转化成简单的数学模型。
设三位同学编号1,2,3,三张卡片编号1,2,3,三张卡片的组合方式共有6种,123,132,213,231,312,321。根据题目叙述,恰有1位同学分到相应卡片的情况有3种,132,321,213,答案为1/2。
小学生在解题中,可以发现符合条件的情况是轮换对称的。如果把题目改成:100个同学拿100张卡片,恰有一位同学拿到自己的卡片的概率。这样学生就可以学到排列组合的基础知识。一位同学拿到自己的卡片,后面的同学拿到不是自己的卡片。100张卡片,排列给100个人,有A(100,100),也就是100!阶乘个情况。第一个同学拿到自己的卡片,第二个同学拿到不是自己的卡片,依次类推,有98!个情况,根据轮换对称性,乘100。恰有一位同学拿到自己的卡片的概率,列式为98!*100/100!=1/99。通过这道题,小学生就掌握了排列组合的全排列知识,也给以后的代数学习打下了基础。得出结论,n个同学拿n张卡片,恰有一位同学拿到自己的卡片的概率是1/(n-1)。

二次多项式因式分解是初一知识,有些地方小学六年级已经学完。但这道题不需小学六年级,这道题只考了命题真假之间的矛盾,以及个位数的加减法和正负数。
题目指出,只有一个假命题。可以看出甲,乙,丙是不能同时成立的。如果丙成立,甲乙至少有一个不成立。如果甲丙成立,则乙不成立。如果乙丙成立,则甲不成立。所以,丁一定是真命题。
所以两个根是异号的。分情况讨论(1)甲乙成立,这与丁矛盾。排除(2)甲丙成立,x=1,另一个x=1。这与丁矛盾。(3) 乙丙成立,x=3,另一个x=-1,符合丁。所以,只有甲是假命题。

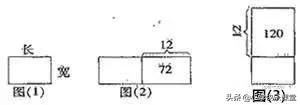
从表面上看,这是一个多项式,但实际考察了两个小学数学知识。第一是最简单的等比数列。两个数之间的比例相等,比如2,6,18,54……,这就是等比数列。这道题是一个等比数列的和的展开式。第一项是(1 x)^2,公比是(1 x)。小学数学有一个基础知识,如何给等差数列和等比数列求和。小学数学考试的计算题第一题经常是数列求和。给等比数列求和,就是给数列的所有项乘公比,再作差即可。
我们计算等比数列的和,得到

。下面是本题考查的第二个知识,我们在数线段、数三角时候学的排列组合乘法原理。求x^2的系数,分母是x,分子是x^3。分子有左右两个因式,右式取x^2,左式需要取x,从8个(1 x)的因式取1个x,有8种取法。
右式取2x,左式需要取x^2,从8个(1 x)的因式取2个x,有8*7/2=28种取法。28*2x=56x。
右式取1,左式需要取x^3,从8个(1 x)的因式取3个x,有8*7*6/3*2=56种取法。
所以本题答案就是这三种情况加在一起,120种取法。

这道题和常规的高中立体几何不同,很多学生看到题就不会做。为什么呢?因为这也是一道考察小学数学背景的题目。本题形式新颖,但对高中生做还是小学生做,难度是一样的。这道题有几个小难点,需要一定思考才能解决。
第一个难点是极限思想,这道题球的半径是5,而底面的半径也是5,所以底面恰好在直径的圆周上。这需要你想到这种极限情况。

接下来,我们沿纵向从直接的圆周,切开球的截面,就知道了本题考查的是平面图形,如图所示。根据勾股定理,已知5和4,求得圆台的高是3。那么,如何求圆台的体积?第二个难点是需要有判断立体图形截面图的空间思维。空间思维是小学科学、机械、美术等学科都必须涉及的教学内容。
我们如图可看出圆台的形状是两个圆锥的差,从截面图中将圆锥补充完整,即可利用圆锥的体积公式,求出两个圆锥的体积之差=1/3(π5*5*15-π4*4*12)=61π

这题比上题简单,正方体是最简单的考法,学生即使没训练过空间思维,在橡皮上画图也可直接解答。学生能想象或绘制出正方体的立体图,即可判断正方体上和正方体内哪些直线是相互平行、垂直。
如果把这道题改一下:正二十面体上的棱,可以构成多少对平行线?这就是一道小学竞赛题。需要学生想象正二十面体的空间形状,判断正二十面体的对棱平行。正二十面体有30条棱,每条棱有一个平行的对棱,所以答案为30。

这道题仍然是小学概率题的列举法,无论对小学生还是中学生都是送分题。题目问1,2至少1个调整的概率,就是1减去1,2都不调整的概率。1-0.9*0.8=0.28。
第二问是期望,小学生如果还没学过期望的术语,但应理解期望的别名“预期的均值”。三个部件调整的概率分别是0.1,0.2,0.3,那么预期总共调整几个部件?这个均值就是0.1 0.2 0.3=0.6。学生如果不理解,可以先问,掷三个骰子,点数之和的期望是多少?学生可以发现3.5 3.5 3.5=10.5。数学家卡尔达诺就是最早通过掷骰子提出并记录了期望的概念。

这道立体几何本质又是一道小学题。第一问考察的是阅读理解,题目给出了正四面体的曲率计算公式。第一问四棱锥的曲率。正四面体的公式是4*(2π-3*π/3)。
正四面体有五个顶点,首先要5*2π。底面有四个顶点,每个顶点有三个面角,分别是90度,45度,45度,共计4*(π/4 π/4 π/2)=4π。另外一个顶点,有四个面角,都是90度,共计4*π/2=2π。所以,正四棱锥的曲率套用公式得5*2π-4π-2π=4π。
第二问问任何多面体的情况。题目给出了欧拉公式。V顶点数-E棱数 F面数=2。欧拉公式在初中课本和一些小学教材上就有,学生应该知道,所以这个提示是多余的。题目给出这个提示,就是直接告诉你此题的解题方法是要套用这个公式,也就是要把这道题的分数送给你。但如果稍加难度,不提示这个公式,学生也应该知道,问任何多面体有关的问题,先要考虑欧拉公式。
第二问如何套用公式,采用的是在高一化学学习原子结构时,一个基本的方法叫均摊法。小学数学的一些空间思维题就有这个方法。例如足球是由五边形和六边形组成的多面体,六边形是20个,问五边形多少个?答案是12个。这是我小学时一道小学奥赛题,距今已经20多年了。还有碳60有60个顶点和32个面,其中12个为正五边形,20个为正六边形。这是一套中学化学题。解决这种多面体的结构问题,方法就是均摊法。多面体的任何一条棱都被两个面公用。
根据题目的公式:总曲率=2πV-所有面内角和。题目要证明总曲率为4π,那么V-所有面内角和/2π=2,需要证所有面内角和=2π(E-F)。另外一个小学知识,是多面形内角和(n-2)*2π,所有面内角和加在一起,是-2πF π面数和。根据均摊法,2E=面数和。就可以得出所有面内角和=2π(E-F)。
总结:小学数学是数学的基础,是纯粹的数学。一些高中生采用题海战术,数学成绩不佳。因为他们在小学时没有打好基础,内功不足。所以,小学数学的教育切不可降低要求,否则会给今后的数学学习带来隐患。这次八省联考的考试,仅凭小学数学知识能解答的题目有54分。而其他题目也不乏需要小学数学的基础。而这次考试的平均分在50左右,说明大部分高中生通过题海战术都处在这个分数段。学数学应该“四两拨千斤”。如果他们能在小学时接受更多思维的拓展,在学习数学最好的年龄段练好内功,他们在高中就不需要题海战术,只需要有的放矢地扩充数学体系。对于智商中等的学生来说,打好小学数学基础,这次考试的平均分应该达到110-120分左右,再补充高中数学的知识点,这张试卷取得满分只是仔细程度的问题。这张试卷并没有考察复杂的思维能力,仍然是只涉及高中基础知识和简单思维的低难度试卷。
,