女士们,先生们,老少爷们儿们!在下张大少。
本文的主要工作是研究一系列波斯马赛克设计,这些设计出现在古老的卷轴上,或是装饰在古老建筑的表面。这些设计中的共同元素是一个特殊的十角星形多边形。为方便起见,这种特殊的凹多边形被称为十角星,是一系列多边形密铺图案的主要几何形状,这些图案都由相同的元素组成。
1 引言
从过去遗留下来的一些文献中可以看出,波斯及其周边地区中世纪建筑表面图案的设计者都具备相当高水平的应用几何学知识。然而,他们都没有表现出同样程度的努力或兴趣,通过证明定理和建立关于此类设计的数学事实,来提供科学的绘制方法。设计师和工匠最关心的是视觉上的和谐与平衡,不仅在细节上,而且在整体上。但是,今天我们所发现的这些设计,几乎没有给研究人员留下什么空间去假设是偶然事件或纯粹的经验。有些技巧只有数学家才能掌握和理解。一个拥有这种详细技术知识的人可以是数学家、艺术家,也可以是任何人。
2 使用特殊的十角星形进行密铺

图1
图1:上:十角星拼块的直尺圆规结构;左下:由该拼块组成的密铺;右下:伊朗克尔曼Masjid-i-Jami清真寺墙壁上的密铺图案。
图1展示了一种创建密铺设计的方法[4]。先绘制一个(10, 3)星形多边形——这是一个将圆上10个等距的点中的每3个顶点朝一个方向连接起来形成的图形(图1中左上角圆内的星形)。通过延伸构成(10, 3)星形多边形的一些线段,并将其与垂直于其他一些线段的线相交,就实现了矩形框架和框架内其他必要线段的构建,如图1右上。这个矩形拼块密铺了整个平面,并创造了一系列令人愉悦的星星,这些星星以列和行的形式排列。
在图1所示的密铺中,特殊的十角星形是密铺的主要几何形状,它可以通过两个同心全等正五边形的旋转独立创建,它们彼此之间的径向距离为36°(图2a、b)。两个正方形的径向距离为45°的这种旋转创造了吸引人的、广泛使用的8点星形多边形(称为八角形),这种多边形在波斯建筑和世界各地的许多几何设计和密铺中都作为十字八角形密铺出现(图2c、d、e)。因此,我们可能会认为,与可以在正方形框架中定义的不太复杂和直接的十字八角形密铺相比,使用这个10点星形(为方便起见,称其为十字星形)创建拼块设计对设计师来说是一个挑战。
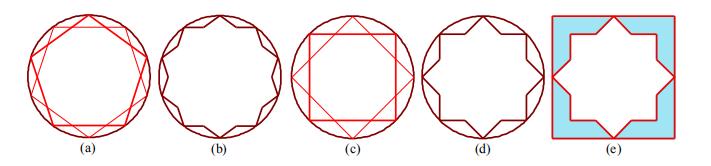
图2
图2:(A)两个同心五边形,(B)生成十角形,(C)两个同心正方形,(D)生成八角形,(E)十字八角形密铺的拼块。
研究过去的文献发现,在大多数情况下,与图1右上所示类似的基本区域是存储在卷轴(Tmār)和小册子(Daftar)中的形状,作为在表面上执行实际密铺时使用的设计,或者作为互锁星形多边形图案的几何实验。这样的基本区域在波斯建筑中被称为结(Girih)。

图3
图3:(左)伊朗伊斯法罕的Imamzeda Darbi Islam,(右)5个Sâzeh模块的拼块。
图3(左)中波斯建筑墙壁上的密铺。包括一个十角星图案。还有其他形状的拼块。事实上,正好有五个主题(模块)。图3(右)展示了这些模块。它们在伊朗被称为Muarraq,一个阿拉伯语单词。这些手工切割的釉面拼块的阿拉伯语单词是Zellij。在此处,它们被称为“Sâzeh拼块”(波斯语意为结构)。
这些模块都有自己特定的波斯语名称。Torange(四边形拼块)、Pange(五边形拼块)、Shesh Band(凹八角形拼块)、Sormeh Dân(蝴蝶结拼块)和Tabl(十角形拼块)。
比较图1和图3中的两种密铺,人们可能会注意到,尽管在两种密铺中使用的单独的Sâzeh模块是相同的,但它们是非常不同的密铺。
图3中拼块的几何结构的绘制方法,经过了一些工艺上的修改,来自专业工匠Maheronnaqsh,他从几个世纪的祖先那里继承了他的职业,最容易接触到过去原始工匠的作品[12]:
通过创建从A发出的4条射线,将直角∠A划分为5个全等角。选择第二条射线上的任意点C,逆时针方向从C垂直于∠A角的两侧。这将产生矩形ABCD以及此矩形内的4条线段,每个线段的一个端点在A处,其他端点是4条射线与矩形ABCD的CB和CD两侧的交点。找到E,即从第四条射线创建的第四条线段的中点。构建一条圆弧,圆弧的中心为A,半径为AE,与F上的AB和G上的第二条射线相交(第二条线段现在是矩形的对角线的一部分)。画一条平行于AD的直线,穿过G,它与第一条射线在H点相交,与第三条射线在I处相交。直线FH通过点E,在J处与AD相遇。构造一条穿过J的直线,与第三条光线平行。还要修建EI线。从F到第三条光线形成一条平行线,在K处与第一条光线相交。构建线段GK、GL和EM。找到N个这样的方法,使GI = IN。画一条穿过N的线,平行于GK,与J发出的线相交,找到P来完成常规的五角形EINPJ。直线DN在Q处与AB的垂直平分线相交。从Q处构造一条平行于FK的直线,使射线MI在R处相交,然后完成该图(图4左)。

图4
以矩形ABCD的中心O作为180°旋转的中心,可以制作图3中密铺的基本区域。图4中的最后两幅图像显示了一个拼块及其密铺,这就是图3中的密铺设计。

图5
图4中的构建方法使用了径向网格方法,作为中世纪时期使用的一种方法,该方法得到了一些图片及其构建说明的支持,这些图片及其构建说明记录在700年前的波斯数学文件《相似或互补图形的交错》中[1]。图5是使用作者创建的径向网格方法逐步构建星形图案设计的示例。

图6
在一些文献中,引入了另一种技术,即“接触多边形法”(PIC)[9],在最近的一些文章[2,3]中对其进行了解释。这是另一个系统,有证据表明设计师在历史上使用过这个系统[2,3]。图6从左到右展示了这种技术,从底层的多边形网络开始,到最后的图案结束,这与图5中构建的图案相同。
3 米尔扎·阿克巴建筑卷轴的密铺及其构造
图1和图3中的两个不同的密铺是由同一组Sâzeh模块组成的,这就提出了一个问题:是否还有更多的密铺是由同一组十角星及其互锁多边形组成的?

图7:米尔扎·阿克巴卷轴的密铺图
图7中的图像精确地呈现了米尔扎·阿克巴藏品中所展示的设计。在此密铺中,十角星彼此相距较远。使用第2节中构建设计所涉及的步骤,我们可以找到此密铺的传统径向解决方案。
不难发现,与图4中的矩形相比,这种密铺的基本矩形具有更长的长度。所以从将直角分成5个全等角的辐线开始,在第一条射线上逆时针选择任意点P(而不是前面问题中的第二条射线)。对于刻在十角星图形中的圆的半径,选择了从第三条射线创建的线段的一半,即线段AM。然后采用类似的方法创建图7中的密铺。图8展示了一个逐步的可视化解决方案。

图8
4.用于构造密铺的正方形Girih
在将直角分成5个全等角的任意一条射线上定位任意一点,并将垂线投到直角的两边,会得到两个不同的矩形:
I. 选择第一条射线上的任意一点C,并将两条垂直线BC和CD放到直角A的两侧。得到矩形ABCD(图12左),其中对角线AC和边BC之间的关系是AC/BC=2 = 1 5,其中 是黄金比例。因此,AB/BC=(5 25) 。
II. 选择第二条射线上的任意一点F,将得到矩形AEFG(图 12左),这就是黄金分割线。AE/EF =

图9
现在的问题是,使用上述同样的技术,我们是否能够想出一个由图3右中所有5个Sâzeh模块组成的新图案?
一个有趣的问题是考虑将正方形作为girih的解决方案。很明显,将A分成5个全等角的射线都不能直接帮助我们。选择P作为A的角平分线上的一个任意点并构造正方形AHPK也不能帮助我们(图9右)。然而,如果我们从一个以A为中心、半径为任意的弧开始,我们就能得到一个解决方案。这条弧线在某些点上切割射线,用来寻找解决方案。图10中的图片,从左上角开始到右下角结束,展示了作者对这个问题的一步步解决。

图10
图11是基于图10中的正方形 girih,由5个Sâzeh模块创建的一个密铺图。该作品于2012年1月在美国马萨诸塞州波士顿举行的AMS-MAA联合数学会议上展出[5],并在马里兰州陶森大学举办的2012年Bridges数学艺术展上展出。

图11
5. 密铺设计中的模块化设计方法
5.1. 基于颜色对比的模块化设计:图12的Kharragan I(2011年1月)是作者根据伊朗西部Kharragan的11世纪双子塔之一的设计创作的艺术品。这件艺术品展示了两种不同的方法,人们认为这两种方法在几个世纪前就被用来创建图案的布局,这是艺术品的中心。从左到右,艺术品展示了基于圆规直尺的设计结构。从右到左,我们看到了另一种方法,基于颜色对比度的模块化设计方法,通过剪切和粘贴两种颜色的拼块来构建相同的设计。这两种构造方法在[16]中提出。

图12
5.2. 基于多边形组合形成图案的模块化设计。图13(中)“希望”是作者的一幅作品[7],它基于模块化设计的概念,使用了两个三角形,每个三角形由较小的三角形和菱形组成,每个三角形由三种颜色的小三角形和菱形组成。真正的拼块装饰在伊朗伊斯法罕的Bibi Zinab陵墓的墙壁上。请注意,在图13(左)中,除了角之外,两个复合三角形(girih模块)的颜色相反。以旋转的方式使用这两个girih模块,产生了图13(中)这幅作品中图案。要制作这种图案的拼块,工匠可以使用如图13(右)所示的切割Sâzeh拼块。

图13:(左)用于查找密铺布局的两个模块;(中)“希望”;(右)用于创建此图案的sâzeh拼块。

图14
6互锁星形多边形密铺的模块化设计
Jay Bonner解释了“多边形系统”,即“接触多边形”,这是过去在创建图案时使用的方法(参见图6)[2]。图14说明了构成五重系统的10个多边形。在这种方法中,工匠制作一个由图14中的模块生成的底层多边形阵列(图6左)。然后,他使用多边形的中点来发现形成新密铺图案的新线条(图6中)。创建过程完成后,把初始多边形阵列擦除即可(图6右)。
在图15(达布伊玛目,伊斯法罕)中,Bonner注意到一组线条将十角星的中心连接起来,与更大的复合拼块形成另一个密铺(这些线条被加粗,更加清晰可见)。他在处理中世纪波斯马赛克设计中的自相似性时使用了这个图形。

图15
最近几年出现的一本关于马赛克设计及其历史的资料丰富的书是《托普卡皮卷轴》[14]。这本书包括了托普卡皮卷轴上的所有图像。该卷轴呈现了114幅用于创建设计的图像。Bonner使用了托普卡皮卷轴的第28号图片(图16左)作为5重自相似A型的另一个例子:“托普卡皮卷轴中的图案28是5重自相似A型设计,其也描绘了在二次设计的创建中使用的底层多边形子网格。这种特殊的技术在历史上曾被使用过,这一点在托普卡皮卷轴中得到了证实。该卷轴的图案28利用红色小点来区分次级图案的下方多边形子网格。”[2]

图16:(左)Topkapi卷轴中的图案;(右)girih拼块集
Lu和Steinhardt也注意到了这些红色的虚线。他们提出,这些虚线展示了一组新的拼块,其中黑色实线决定了这些新拼块上的每个设计[11]。他们意识到,这个新的集合可以作为一组模块,类似于上一节中提出的模块,但现在的形式更加复杂,用于寻找新的互锁星形多边形图案。这消除了圆规直尺构造所涉及的困难,事实上,为创造更多有趣的马赛克图案打开了大门,这些图案不是以通常方式形成的。Lu和Steinhardt将这种新的组合称为girih拼块。这是我们在本文中对构成波斯马赛克拼块布局的所有模块所使用的名称。
使用这个集合中的3个模块将使我们能够构建使用圆规直尺构建的上述4个密铺。在图17中,从左到右,我们发现图16中5个模块的3个girih模块的组合如何分别生成图1、图4、图7和图11中的密铺。
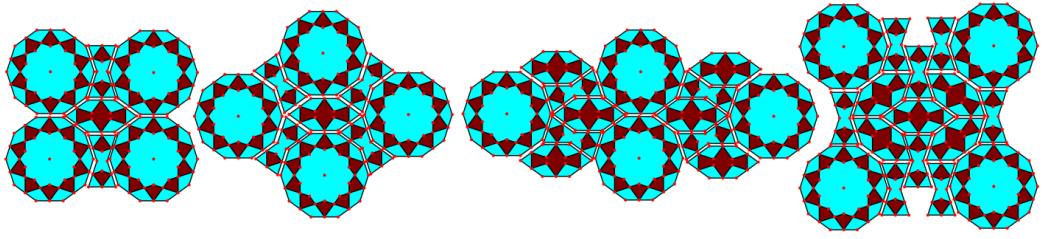
图17
显然,图15中的设计非常复杂,而且比图17中的其他4个密铺要复杂得多。然而,使用girih模块集可以比使用圆规直尺更容易地构建它。图18显示了如何构建更大的密铺拼块。然后,工匠在墙上完成整个密铺只是时间问题。
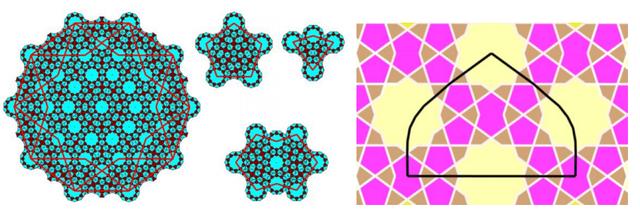
图18
彭罗斯发现了风筝和飞镖这两种拼块,每个拼块都由一些弧线设计,只能非周期性地拼合(没有过渡性对称)(图19中)。这两块拼块形成了一个菱形,这个菱形是一个五重对称星形的一翼,可以用(10,3)星形多边形来构造(图19左)。为了正确地使用风筝和飞镖拼块,还应该正确地连接拼块相同颜色的弧线,以形成连续的曲线(封闭或开放)。基于John Conway[8]创造的一组复合拼块,Lu和Steinhardt提出了3种新的拼块,类似于girih拼块中的三种,并产生了彭罗斯密铺(图19右)。

图19
使用图19右中的这个新集合,并用图16右的Girih拼块替换它们。Lu和Steinhardt在一些波斯拼块中提出了一种可能的准周期性结构。早在几年前,Makovicky[13]就注意到并分析了类似的准周期模式。此外,Rigby[15]发现了一种方法,可以在风筝和飞镖的表面覆盖适当的Sâzeh拼块,以产生各种非周期性的连锁图案。然而,图16中Girih拼块的发现无疑是马赛克设计研究中的一个显著点。
请注意,通过使用Rigby建议的拼块,可以以拼块非周期性地密铺平面的方式制作3个girih模块(图20)。

图20
观察图16中的类似设计,人们可能会得出这样的结论:过去的设计者在寻找最大的对称性,特别是局部和全局的旋转对称性,尤其是5重和10重的旋转对称性,而不是其他东西。所以他们的一些马赛克设计吸引了现代晶体学研究人员,他们发现了类似的图案。
需要注意的是,彭罗斯拼块不能产生整体或局部10重旋转对称。它们只能形成5重对称。彭罗斯密铺有无数种。除了两个以外,没有一个具有全局5重旋转对称性。这两个具有全局5重旋转对称性的密铺称为“太阳”和“星星”。图21左是太阳密铺。图21右是与Rigby拼块覆盖相同的密铺。图21右中密铺的中心圆形部分。包括从中心等距的第一系列十角星图形,类似于图18左中的十边形图形。然而,这个太阳的更大部分只保持5重的旋转对称,但是图18左中的十边形有10重的旋转对称。

图21:彭罗斯太阳和Girih太阳
参考文献
[1] Anonymous. Interlocks of Similar or Complementary Figures. Paris: Biblioth`eque Nationale, ancien fonds. Persan 169, ff. 180r–199v.
[2] Bonner, J., Three traditions of self-similarity in fourteenth and fifteenth century Islamic geometric ornament, Proceedings of the ISMA/Bridges: Mathematical Connections in Art, Music, and Science, R. Sarhangi and N. Friedman, eds, Granada, Spain, 2003, pp. 1-12.
[3] Cromwell, P.R., The search for quasi-periodicity in Islamic 5-fold ornament, Math. Intelligencer 31, 2009, pp. 36 – 56.
[4] El-Said I. and A. Parman, Geometric Concepts in Islamic Art, World of Islam Festival Publishing Company, London, 1976.
[5] Fathauer R. and Nathan S Nathan Selikoff, eds, Joint Mathematics Meeting Art Exhibition Catalog 2012, Boston.
[6] Fathauer R. and Nathan S Nathan Selikoff, eds, Bridges International Conference Art Exhibition Catalog 2011, Coimbra, Portugal.
[7] Fathauer R. and Aklaman E., eds, Bridges Art Exhibition Catalog 2009, Banff, Canada.
[8] Gardner, M. Pentose Tiles to Trapdoor Ciphers, MAA, 1977
[9] Hankin, E.H., The Drawing of Geometric Patterns in Saracenic Art, Memories of the Archaeological Society of India, Vol. 15, Government of India, Calcutta, 1925.
[10] Kaplan, C.S., Islamic star patterns from polygons in contact, Graphics Interface 2005, ACM International Conference Proceedings Series 112, 2005, pp. 177-186.
[11] Lu, P.J. and P.J. Steinhardt, Decagonal and quasi-crystalline tilings in medieval Islamic architecture, Science 315, 2007, pp. 1106 – 1110.
[12] Maheronnaqsh, M., Design and Execution in Persian Ceramics, Reza Abbasi Museum Press, Tehran,1984.
[13] Makovicky, E., In Five Fold Symmetry, I. Hargittali, ed, Word Scientific, Singapour, 1992, pp. 67-86.
[14] Necipoğlu, G., The Topkapi Scroll: Geometry and Ornament in Islamic Architecture, Getty Center Publication, Santa Monica, USA, 1995.
[15] Rigby, J., Creating Penrose-type Islamic Interlacing Patterns, Bridges International Conference Proceedings, Reza Sarhangi and John Sharp, eds, London, UK, 2006, pp. 41-48.
[16] Sarhangi, R., S. Jablan, and R. Sazdanovic, Modularity in Medieval Persian Mosaics: Textual, Empirical, Analytical, and Theoretical Considerations, Bridges International Conference Proceedings, R. Sarhangi, ed, Winfield, Kansas, 2004, pp. 281-292.
[17] Reza Sarhangi, Polyhedral Modularity in a Special Class of Decagram Based Interlocking Star Polygons
青山不改,绿水长流,在下告退。
转发随意,转载请联系张大少本尊。
,




