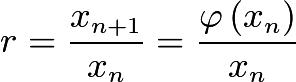[遇见数学创作小组] 作者徐琳,数学教师。
今天的主题是几何,大自然的几何,一说到几何,大家肯定不陌生,三角形,正方形,圆等,但是自然界中的形状都是三角形,正方形和圆吗,并不是,经典几何学所描绘的都是由直线或曲线,平面或曲面所构成的各种几何形状,他们是显示世界中物体形状的高度抽象。伽利略说:大自然的语言是数学,它的标志是三角形、圆和其他图形。但是对于了解大自然的复杂性来讲,欧几里得几何学是一种不充分、不具有普遍性的抽象。
在 Mandelbrot 1975年出版的《大自然的分形几何学》一书中,有这么几句话:“云不只是球体,山不只是圆锥,海岸线不是圆形,树皮不是那么光滑,闪电传播的路径更不是直线。它们是什么呢?它们都是简单而又复杂的‘分形’……”分形的提出是为了更好的去描述、解释真实的大自然。也正因为此,Mandelbrot被称为“分形之父”。
最著名的分形问题是海岸线到底有多长,Mandelbrot给出的答案是:海岸线的长度是不确定的!海岸线的长度取决于测量时的尺度,就好比同样是一段路,大象和蚂蚁测量的步数绝对差很多,这是因为大象忽略了细节,而蚂蚁的路程远大于大象,这好像又给龟兔赛跑一个更合理的理论依据。
如果你仔细看一下这几幅图,你会很快总结出来分形的特征,那就是具有自相似性;具有无穷多的层次;和通常可以由一个简单的,递归、迭代的方法产生出来。
简单的、递归、迭代,只要你稍微熟悉些高中数学好像对这些定义就不陌生,没错!数列!如果说上面是图形的迭代让人很有距离感,那么数字的迭代就会很亲切。
第一次介绍分形是在高一讲授数列极限的时候,我是以这样一个问题引入:是否存在这样一个图形,具有有限的面积却拥有无限的周长?当学生找不到答案的时候,此时我会带着学生从一个正三角形(边长为 l )开始,根据下列规则进行构造:
步骤 1: 将其每边三等分;
步骤 2: 以中间的 l/3 段为边向外作正三角形;
步骤 3: 将第二步中的 l/3 边长去掉,得到一个新的多边形。
然后把这个过程无限继续下去.
接下来,计算一下无限次后的图形周长和面积。
第1次分形后周长
第2次分形后周长
第3次分形后周长
……
第 n 次分形后周长
同理可得,第 n 次分形后面积
当n趋向无穷次周长与面积:
所以我们得到了无限次后的图形周长是无穷大的,但是面积确是有限的。像这样的图形还有很多,我们把这类图形叫做Koch曲线。同时可以得到数列极限的收敛与发散的条件。
上面边两张图分别是公比 r>1, r<-1。
上面两图公比为 0<r<1, -1<r<0。
因此,我们总结出对于等比数列,当 |r|<1,数列收敛,lim a_n=Constant;当 |r|>1,数列发散,lim a_n=∞。
为了更好的理解这种迭代过程,下面会通过数据和图形给大家一个直观的感受。
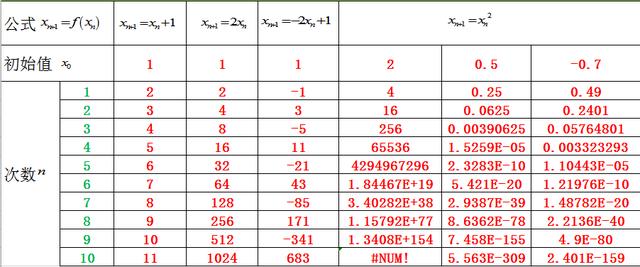
分别选择几种常见的函数,作为迭代公式,在给定一个初始值的情况下,我们看一下迭代 10 次后的一个效果。
对于一次函数,如果系数大于1,则迭代结果越来越大,反之,对于
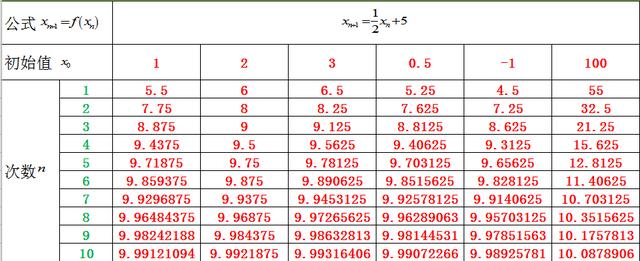
不管初始值在哪里,10 次迭代后都接近 10,如果类比上面的等比数列,一次函数的斜率可近似看做等比数列的公比,这里注意,一次函数中如果有常数项,则不是等比数列。但我们仍可以近似理解为比例,因为当 xn 无穷大时,常数项可以忽略不计。所以当 |r|<1,收敛;|r|>1,发散,似乎仍然有效。
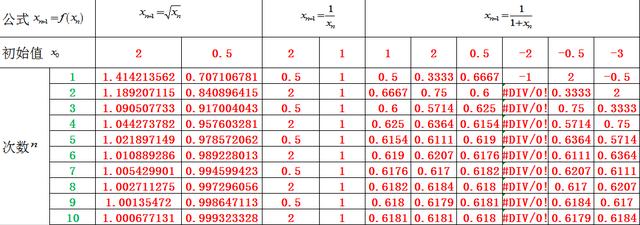
但是当迭代包含平方,根式,分式等关系时,我们仍发现结果存在发散和收敛的情况。当我们观察的函数不局限等比等差这种规范的关系时,给出任意非线性函数,以及不同的初始值,发现在某些情况下,不断迭代的结果会趋向于一个定值,而这个值我们在数值分析中称为不动点,不动点迭代(Fixed point iteration)指的是:选择适当的初始值 x0,按照如下的迭代格式计算,
,n=0,1,2...,如果数列 {xn} 有极限
则称迭代是收敛的,x^* 是非线性方程的根和 φ(x) 的不动点。
那么对于不同的函数,什么样的情况下收敛,我们可以通过迭代回形图试着寻找一下。
以上两种情况是收敛的,我们发现 φ(x) 在 x^* 附近较平缓;
以上两种情况是发散的,我们发现 φ(x) 在 x^* 附近较陡峭。
如果结合我们之前总结的等比数列当公比,则数列有极限,类比到一般函数,此时的
,结合导数定义,因此我们可以联想到或许当 |φ'(x^*)| <1时,函数 φ(x) 收敛且有不动点。
在得到不动点结论的过程中,我们并没有严格的证明,更多的是一步步探索发现和总结,如何从问题的表向到本质,再从本质到外化,即从特殊到一般,再从一般理论到应用,这应该是发展的一般规律,也是学习的自然过程。
最后再回到分形,“分形不仅展示了数学之美,也揭示了世界的本质,还改变了人们理解自然奥秘的方式。”在分形的世界中,每个人都可以是艺术家。
如果给你这样一幅画,你会不会以为这是出自哪个抽象派画家之手,但实际上这个形状仅仅出自一个纯数学的练习。Mandelbrot在TED演讲中曾介绍过分形和混沌,他总结的最后一句话。
Bottomless wonders spring from simple rules,which are repeated without end. - Benoit Mandelbrot无边的奇迹源于简单规则的无限重复。——本华·曼德博
,