中心极限定理是在统计学中除了大数定理的另一块基石,有着极为重要的意义和广泛的应用空间,本文就以通俗的案例来讲解什么是中心极限定理,中心极限定理的数据演示以及中心极限定理的应用。
什么是中心极限定理?
中心极限定理就是随机样本的均值总是围绕在总体均值周围,且呈正太分布。
先举个栗子:
现在要统计燕山大学2015年8000名毕业生三年后的平均薪资情况,把所有的毕业生都调查一遍的话成本太高,现在我们调查25组,每组40人,一共调查1000人,然后求出每一组的平均值,中心极限定理就是说,这些均值呈正太分布,而且随着每组样本的增加,效果会更好。把这些平均值相加再求均值,这个均值就非常接近总体均值了。
其中有几个点需要注意一下:
- 不管总体是怎样的分布,最后每组的均值还是呈正太分布
- 样本每组要足够大,但也不需要太大,取样本的时候,一般认为,每组大于等于30个,即可让中心极限定理发挥作用。
用实际数据来演示中心极限定理
注:使用python来模拟数据,不懂的同学可以略过代码
生成数据:我们用掷骰子这一概率论中经常用到的道具来演示,用python模拟掷100000次骰子,并求总体平均值。
import numpy as np
import pandas as pd
shaizi_data=np.random.randint(1,7,100000) #生成掷骰子随机数据
print(shaizi_data.mean()) #打印平均值
print(shaizi_data.std()) #打印标准差
import matplotlib.pyplot as plt
var=np.bincount(shaizi_data) #频次统计
plt.bar([1,2,3,4,5,6],var[1:],0.5) #绘制条形图
plt.show()
平均值:3.5049 ,标准差:1.697(每次生成数据都会有细微的差别)
把生成的数据用条形图图展示出来是这样的:1~6的分布都很均匀,ok~

10万次掷骰子频数分布直方图
下面就是见证奇迹的时刻,我们要在此数据集上来验证中心极限定理:
先抽取1000组数据,每组100个样本,结果见下图:
分组均值的均值:3.498,分组均值的标准差:0.167
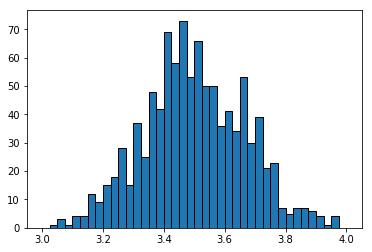
抽样均值的分布规律
那在不同的组数与组内样本数量的情况下,是不是都是这样的呢,下边就限定组数进行对比,每组100个样本,分别抽取50组,100组,1000组,10000组来观察数据,以下是代码实现:
for m,k in zip([50,100,1000,10000],[221,222,223,224]): #限定不同的组内样本数
n=1000
s=[]
for i in range(n):
x_=0
for i in range(m):
x=shaizi_data[int(np.random.random()*100000)]
x_=x_ x
x_=x_/m
s.append(x_)
s=np.array(s)
print(s.mean())
print(s.std())
plt.subplot(k)
plt.hist(s,40,range=[3,4],edgecolor="black")
plt.show()
图见下方:

相同样本数,不同组数的抽样结果
组数 均值 标准差
50 3.518 0.173
100 3.488 0.162
1000 3.495 0.172
10000 3.490 0.171
随着组数的增多,样本均值的均值就越来越靠近总体均值,也就是说,在可以的情况下,取样的组数尽可能多,那么样本均值就越能够代表总体均值。
下边再看一下组数不变的情况下,每组内样本数量不同会发生什么变化。一共取1000组,每组数据的样本数量分别限制在50,个,100个,1000个,10000个,看效果:

不同样本数量的随机样本均值分布
每组内的样本个数 均值 标准差
50 3.493 0.240
100 3.499 0.167
1000 3.494 0.055
10000 3.492 0.017
在组数不变,组内样本越来越多的情况下,样本均值的标准差越来越小,样本均值越来越向总体均值靠拢 。
中心极限定理在实际当中的应用主要有两方面:
- 抽样估计:这种情况是我们不能知道我们想要研究的对象的平均值,标准差之类的统计参数。中心极限动力在理论上保证了我们可以只用抽样一部分的方法,达到研究推测对象统计参数的目的。就像上文的例子中,通过调研部分毕业生的薪资水平而推算出整体毕业生的平均薪资。
- 假设检验:这种情况下,是我们已知总体的分布,来计算样本的置信区间,或者规定了规定了样本空间反向计算样本容量。典型的应用场景是,计算炮弹的命中几率。
中心极限定理与大数定理的关系:
大数定理证明了样本平均值趋近于总体平均值的趋势,但是却没有量化样本平均值趋向于总计平均值的概率,而中心极限定理证明了这一点,具体的说明了,随机样本平均数与总体平均数的差值不差过一定范围的概率大小问题。
,




