面积问题








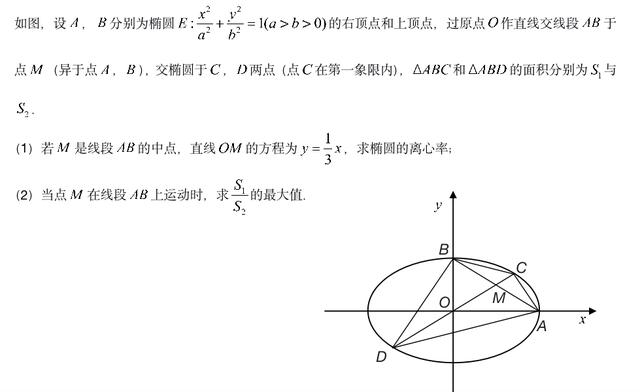



(1)若点B的坐标为(1,3/2),求三角形OAB面积的最大值;
(2)设A(x1,y1),B(x2,y2)且3y1 y2=0,求当三角形OAB最大时,直线l的方程.
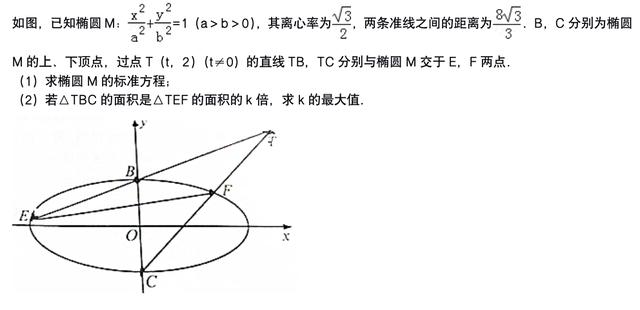
题型六:弦或弦长为定值、最值问题



过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.(Ⅰ)求P点坐标;(Ⅱ)求证直线AB的斜率为定值;(Ⅲ)求△PAB面积的最大值.



(I)求过点O、F,并且l与椭圆的左准线相切的圆的方程;(II)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围。


4、已知点A,B的坐标分别是(0,1),(0,-1),直线AM,BM相交于点M,且它们的斜率之积为-1/2.(1)求点M轨迹的方程;(2)若过点D(2,0)的直线l与(1)中的轨迹C交于不同的两点E、F(D在E、F之间),试求与三角形ODE和三角形ODF面积之比的取值范围(O为坐标原点).