征服世界上最流行的玩具——魔方
文/仅此
鲁比克立方(Rubik’s cube),或称魔方,相信大家多多少少都拧过几下,也有不少人能成功复原最常见的三阶六面魔方。笔者也可厚着脸弱弱地自称为一个前魔方爱好者,练过一阵子三阶速拧,收集并复原过各种异形魔方,其中最爱镜面,超适合耍帅,然至今未能复原那个被我手贱打乱的SSQ1,望大神指点 [拱手状]!

三阶魔方
复原任意状态三阶魔方的最少步数已被证明为20步*,换句话说,任何超过20步的打乱,都可以用更少的步数还原回去,所以给别人打乱魔方的时候不需要再努力地乱转了,并无卵用~[调皮脸]。这一数字有时被称为“上帝之数”,不过装逼的时候最好还是不要只说这个称呼啦,毕竟“上帝之数”有不止一两个代指,对方可能并不会get你的点[摊手]。

镜面魔方
在探索最少步数的道路上,群论(group theory)可谓发挥了至关重要的作用,于是作为群论迷妹的笔者此番来意便是:略去严格的证明不提,带领各位看官感受一下如何从群论的角度来征服魔方!
先来简单解释一下为何魔方会和群论有着如此密切的关系。数学中,群可以用一个集合G配合一种运算(如加法、乘法等)来定义,其中这项运算要满足结合律(以加法为例,即(a b) c=a (b c)),同时集合G要满足以下三点要求:
(1)集合中存在一个元素e使得对集合G中任意元素g,有e与g的运算结果仍为g(如加法中0的地位,乘法中1的地位);
(2)集合中任意元素间运算的结果仍在这个集合中(简称为封闭性);
(3)集合中每个元素g都有唯一对应的相反数g’,使得g与g’的运算结果为e(如加法中相对应的正负数)。举个最常见的栗子:全体整数配上加法运算就满足以上所有条件,因此可以看作一个加法群**

将魔方侧面展开编号
对于魔方来说,存在一个由“全体可能的色块排列”组成的集合,不妨成为集合M吧。为方便研究,我们将魔方展开并编号,这样一来,每一种可能的色块排列都可看作对这些编号的置换(permutation),通俗一点说,就是将编号打乱顺序。例如,将复原态魔方的橙色面(看作前面)顺时针转动90°后(通常记作F转动),就会有19换到21的位置,21换到27的位置,27换到25的位置,25换到19的位置,可记作(19 21 27 25)。依此记下各色棱块角块的置换,F转动后的色块排列可以记作(19 21 27 25)(20 24 26 22)(7 28 48 18)(9 34 46 12)(8 31 47 15)。
置换间的组合即为一种运算,如连续做两次F转动就是进行了一次运算,运算结果是橙色面转动180°的状态,可以用(19 27)(21 25)(20 26)(24 22)(7 48)(28 18)(9 46)(34 12)(8 47)(31 15)表示。不难接受,任何置换(或说转动)的组合结果都会在集合M中。同时这种运算也满足结合律,尽管实际操作上很难看出,但数学上不难验证***
魔方的复原态可以充当集合中e的地位。置换的相反数也很容易得到,只要每个小置换“反着写”就好,如F转动的相反数就是(25 27 21 19)(22 26 24 20)(18 48 28 7)(12 46 34 9)(15 47 31 8),不难看出,这就是将(处于复原态的魔方)橙色面逆时针转动90°后的色块排列。对于更复杂的状态,即使无法确定复原方法,只要写出编号的置换,仍可以轻松写出它的相反数(尽管手动写出置换并不是一件容易的事)。
对照上述“群的定义”,可以发现,集合M是一个群。
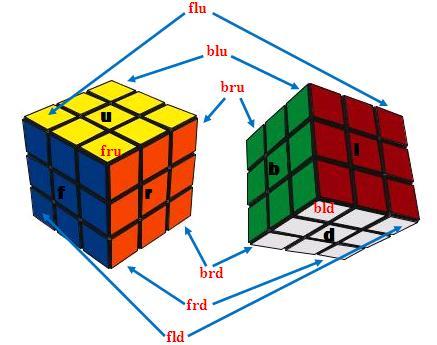
不难理解,一旦我们有了90°顺时针转动白色顶面(U),黄色底面(D),蓝色左面(L),绿色右面(R),橙色前面(F),红色后面(B)的六个基本置换,就可以通过它们之间的运算得出任意色块排列,或说这六个基本置换可以“生成”集合M。当然,在生成的过程中会有不同转动组合得到同一最终状态的情况,不过不必担心,这一问题后续会得到解决。
接下来我们需要准备54×54的阶梯空格子,并按照(列数,行数)的方式标号,见笔者作为灵魂画手所做的下图。我们将把集合M里的元素挨个放入相应的格子中,每格一个。
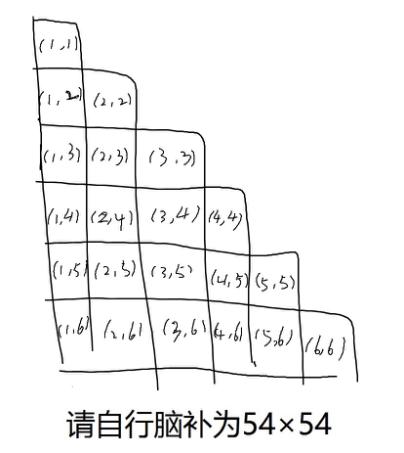
54×54阶梯格
首先我们填入六个基本转动(U,D,L,R,F,B)及它们的相反数,以F转动为例,参与置换的最小数字为7,且7被置换到了28的位置,所以我们将F转动后的这种色块排列填入格子(7,28)。
填好六个基本转动后,我们将格子里已有的六个状态分先后两两组合。所谓分先后就是说,先做U转动再做F转动与先做F转动再做U转动是分别对待的,因为它们会造成不同的色块排列(不好脑补的时候就拿起魔方转一转)。此时如果我们仍按填入基本转动的规则将组合结果填入格子,会发现有些格子已经被占领了,如先U再F组合后的色块排列应该被填在(1,3),然而(1,3)已经填入了U转动。这种时候我们就在原有的U、F组合之后再组合一个U的相反数,这样编号1就会被复位,我们需要确定新的格子。如果新的格子仍被占用,就再组合一次占领新的格子的置换的相反数,直到有空格子让我们填入或得到复原态,一定要按顺序记录好都组合了哪些转动,这是得到复原方法的关键。得到复原态意味着我们最初组合得到的色块排列可以通过另一系列步数等同或更少的转动得到,这就解决了我们之前的担忧。

三阶魔方转动图解
聪明的看官们一定已经猜到了,接下来的工作就是不停地两两组合格子中已有的状态并按照上述规则填入空格子中,直到整张表格不再变化,即任何新的组合都会被简化到复原态。
如此一来,这张表格完成之时,便是我们确定最少步数之日。同时,拥有了这张表格后,理论上只要我们确定了色块排列所对应的置换,将其所在格子中的操作逆向而为就能复原。然而,相信看官们已经发现,此处有个悲伤的消息曰:这张表格非人力所能完成,我们需要向计算机寻求帮助,设定好一定的程序,就能在有限的时间内完成复原。

魔方与计算机视觉识别
So,至此我们终于得到了“暴力”征服魔方的方法,这项方法广泛适用于各式魔方和类魔方玩具****,障碍只在于计算机的算法足不足以在可接受的时间内完成表格的制作。
不过笔者始终认为,真正的暴力征服魔方,是拆了重装啊!红红火火恍恍惚惚[手比V字]

高阶魔方内部结构
【附加说明】
*追求严谨看这里:此处的20步不含(为操作方便进行的)魔方整体翻转,并将单面旋转180°看作一步。我们的方法是将单面旋转180°看作两步,所以总步数要多些,具体数字疏于考证,约在25步上下。
**值得一提的是,群的定义中并不要求运算满足交换律,例中的全体整数满足加法交换律,属于一类特殊群——阿贝尔群。
***置换本质是映射,映射间的复合从定义上满足结合律。
****能用这种方法破解的一类玩具被称为permutation puzzle

基于排列组合的小玩具
订阅“来吧 学数学”头条号 享更多精彩内容
,




