今天来学习数组的插入排序算法。
在讲算法之前,我们先来想象这样一个场景:我们要上体育课,体育老师要求同学们从高到矮排好队。当同学们都排好队的时候,小甲同学迟到了。这时候小甲同学随便站个地方可不行,因为这样队伍就不是排好的了,所以要将小甲同学插入到队伍中,使队伍重新又是从高到矮排好的。小甲同学对比自己和同学们的身高,找到自己的位置,排到队伍里,就完成了队伍的排序。
这个将一个无序元素插入到n个元素的有序集合,使新的(n 1)个元素的集合变成重新有序的动作就是插入排序的基本思想。借助这种思想,我们就可以把一个数组分成有序的和无序的两部分,不断将无序的部分里面的元素取出来插入到有序的部分中,使数组最终变为有序的。因为一个元素本身就有序了,我们可以把第一个元素作为最初的有序部分。
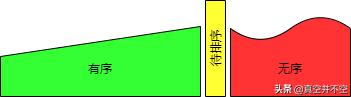
排序示意图
我们来看对数组[6, 3, 9, 7, 8, 5, 0, 2, 4, 1]的从小到大排序过程:
1. 得到一个未排序数组[6, 3, 9, 7, 8, 5, 0, 2, 4, 1]。

2. 得到首元素6,因为只有一个元素,所以直接放入有序部分。

3. 取出下一个元素3,将其依次与有序部分的元素对比,此时有序部分元素只有6,对比后发现3小于6,所以3要作为首元素插入,得到新的有序部分[3, 6]。

4. 取出下一个元素9,将其依次与有序部分的元素对比,发现9比有序部分的最后一个元素6还要大,所以将9插入到有序部分的末尾,得到新的有序部分[3, 6, 9]。

5. 取出下一个元素7,将其依次与有序部分的元素对比,发现7比9小,比6大,所以将7插入到6和9之间,得到新的有序部分[3, 6, 7, 9]。
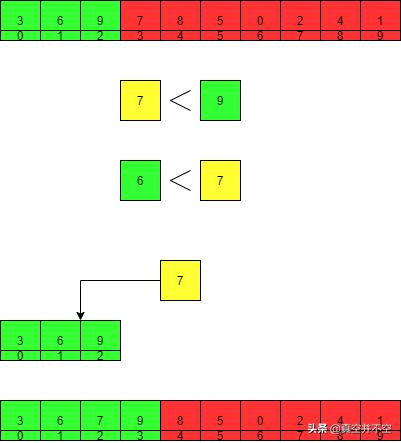
6. 取出下一个元素8,将其依次与有序部分的元素对比,发现8比9小,比7大,所以将8插入到7和9之间,得到新的有序部分[3, 6, 7, 8, 9]。

7. 取出下一个元素5,将其依次与有序部分的元素对比,发现5比6小,比3大,所以将5插入到3和6之间,得到新的有序部分[3, 5, 6, 7, 8, 9]。
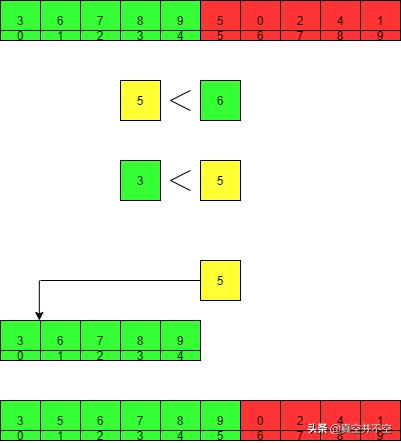
8. 取出下一个元素0,将其依次与有序部分的元素对比,发现0比有序部分的首元素3还要小,所以将0作为有序部分的首元素插入,得到新的有序部分[0, 3, 5, 6, 7, 8, 9]。

9. 取出下一个元素2,将其依次与有序部分的元素对比,发现2比3小,比0大,所以将2插入到0和3之间,得到新的有序部分[0, 2, 3, 5, 6, 7, 8, 9]。
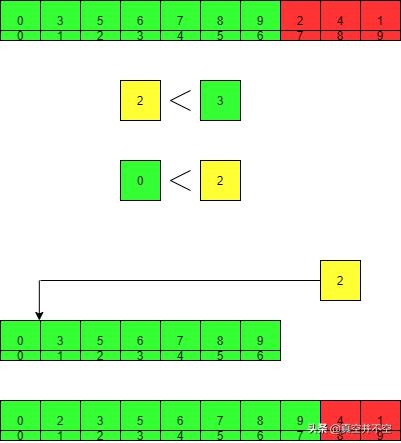
10. 取出下一个元素4,将其依次与有序部分的元素对比,发现4比5小,比3大,所以将4插入到3和5之间,得到新的有序部分[0, 2, 3, 4, 5, 6, 7, 8, 9]。

11. 取出最后一个元素1,将其依次与有序部分的元素对比,发现1比2小,比0大,所以将1插入到0和2之间,得到新的有序部分[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]。

11. 至此,所有元素归入有序部分,排序完成。
算法实现代码如下:
/**
* 数组的插入排序算法
* 从小到大排序
*
* @param nums 待排序数组
* @param lo 排序区间lo索引(包含)
* @param hi 排序区间hi索引(不包含)
*/
public static void insertionSort(int[] nums, int lo, int hi) {
// 数组为null则直接返回
if (nums == null) {
return;
}
// 索引检查
if (lo < 0 || nums.length <= lo) {
throw new IllegalArgumentException("lo索引必须大于0并且小于数组长度,数组长度:" nums.length);
}
if (hi < 0 || nums.length < hi) {
throw new IllegalArgumentException("hi索引必须大于0并且小于等于数组长度,数组长度:" nums.length);
}
if (hi <= lo) {
// lo索引必须小于hi索引(等于也不行,因为区间是左闭右开,如果等于,区间内元素数量就为0了)
throw new IllegalArgumentException("lo索引必须小于hi索引");
}
if (lo 1 >= hi) {
// 区间元素个数最多为1
// 无需排序
return;
}
for (int i = lo 1; i < hi; i ) {
// 获取当前元素
int e = nums[i];
// 从当前位置的前一个元素开始,往前查找,直到索引为-1
// 或找到第一个小于等于当前元素的值(等于时可保证稳定排序)
int j = i - 1;
for (; j >= lo; j--) {
if (nums[j] <= e) {
// 如果找到一个元素小于等于当前元素
// 退出循环
break;
}
}
// 此时j索引表示当前元素插入位置的上一个位置
// 所以插入位置索引为j 1
// j可能为-1,此方法仍然适用
int insertIdx = j 1;
// 如果insertIdx == i,说明此时元素已经就位了,无需插入
if (insertIdx < i) {
// 元素未就位,需要插入
// 插入方法为从insertIdx(包含)到i(不包含)之间的元素往后移一个位置,
// 当前元素放到insertIdx的位置上
System.arraycopy(nums, insertIdx, nums, insertIdx 1, i - insertIdx);
nums[insertIdx] = e;
}
}
}
测试代码如下:
int[] nums = {6, 3, 9, 7, 8, 5, 0, 2, 4, 1};
System.out.println("排序前:" Arrays.toString(nums));
insertionSort(nums, 0, nums.length);
System.out.println("排序后:" Arrays.toString(nums));
输出如下:
排序前:[6, 3, 9, 7, 8, 5, 0, 2, 4, 1]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
符合我们的预期。
,




