题目:
一、 若4条直线两两相交于不同点,则对顶角、同位角、内错角、同旁内角各有几对?
二、 若n条直线两两相交于不同点,则对顶角、同位角、内错角、同旁内角各有几对?
这道题看似不难,真正做起来,还是挺考验逻辑思维和推导能力的。
花了一上午,整理了一下,不知道能不能给神兽讲清楚。
1、 回到起点
若n=1,即只有1条直线,那么不存在相交点,也不存在对顶角、同位角、内错角、同旁内角。

▲图1
若n=2,即只有2条直线,那么存在1个相交点,对顶角有2对,不存在同位角、内错角、同旁内角。

从这里可以看出:对顶角先与同位角、内错角、同旁内角形成,只要有2条相交直线,形成1个相交点,就形成2对对顶角(简化一下:2条相交直线=形成1个相交点=对顶角2对)暂存备用。
若n=3,即有3条直线,那么存在3个相交点,对顶角有6对,同位角12对、内错角6对、同旁内角6对。

▲图3
从这里可以看出:(1)有3条相交直线,同位角、内错角、同旁内角开始形成;
(2)3条相交直线,形成3个相交点,对应6对对顶角;
(3)任意两条直线被第三条直线所截,形成:同位角4对,内错角2对,同旁内角2对。
列举:
蓝、绿两条直线被第三条红色直线所截,形成:同位角4对,内错角2对,同旁内角2对;
蓝、红两条直线被第三条绿色直线所截,形成:同位角4对,内错角2对,同旁内角2对;
红、绿两条直线被第三条黄色直线所截,形成:同位角4对,内错角2对,同旁内角2对;
所以共形成同位角12对,内错角6对,同旁内角6对。
(4)以上可以看出:对顶角和(同位角、内错角、同旁内角)不是一伙的。
对顶角依附于2条相交直接形成,1个相交点对应于2对对顶角。
(同位角、内错角、同旁内角)依附于3条相交直接形成,且同时形成产生,同旁内角对数=内错角对数,同位角对数是他们的2倍。可以理解为他们是绑定在一起的。
2、 进入正题
有了以上的铺垫,再来解题,思路应该已经清晰了。

▲图4
若n=4,即有4条直线,那么存在6个相交点,对顶角有12对。
6个相交点的形成过程是:蓝、绿、红三直线相交形成3个相交点,黑线加入后,分别于他们相交,又形成3个相交点,所以共形成6个相交点。
接下来解决(同位角、内错角、同旁内角)对数:
有两种思路:
第一种思路:以3条直线为一组,可列举出:
蓝、绿、红为一组,形成:同位角12对,内错角6对,同旁内角6对
蓝、绿、黑为一组,形成:同位角12对,内错角6对,同旁内角6对
蓝、红、黑为一组,形成:同位角12对,内错角6对,同旁内角6对
红、绿、黑为一组,形成:同位角12对,内错角6对,同旁内角6对
所以共形成:同位角48对,内错角24对,同旁内角24对。第一小题完成。
第二种思路:
基于“任意两条直线被第三条直线所截,形成:同位角4对,内错角2对,同旁内角2对”的基本单元构成。
从4条直线中任意选出2条直线,有6种可能;剩下2条直线,这2条直线就可以作为第三条直线。那么构成上述基本单位的数量为:6×2=12
所以共形成:同位角4×12=48对,内错角2×12=24对,同旁内角2×12=24对。第一小题完成。
总结:第一种思路做4条直线还是可以的,比较直观。第二种思路是为接下来的第二小题做铺垫的,应掌握第二种思路的解题方法。
3、 再走一步
若n=5,即有5条直线
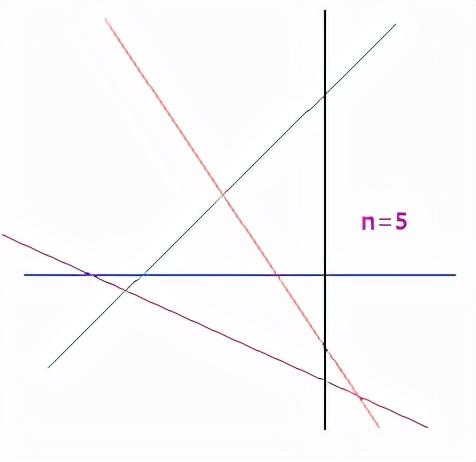
▲图5
4条直线,有6个相交点,第5条直线加入后,就有6 4=10个相交点了。形成20对对顶角。
同理:基于“任意两条直线被第三条直线所截,形成:同位角4对,内错角2对,同旁内角2对”的基本单元构成。
从5条直线中任意选出2条直线,有10种可能;剩下3条直线,这3条直线就可以作为第三条直线。那么构成上述基本单位的数量为:10×3=30
所以共形成:同位角4×30=120对,内错角2×30=60对,同旁内角2×30=60对。
再走一步其实是为解第二小题打基础的。
4、 当n=n
当n=n,即有n条直线两两相交于不同点。
首先来看形成多少个相交点:
n=1,0个相交点
n=2,1个相交点
n=3,3个相交点(加入第3条后,多形成2个交点,即1 2=3)
n=4,6个相交点(加入第4条后,多形成3个交点,即1 2 3=6)
n=5,10个相交点(加入第5条后,多形成4个交点,即1 2 3 4=10)
……
n=n,n(n-1)个相交点[加入第n条后,多形成n-1个交点,即1 2 3 4 (n-1)=n(n-1)]
所以形成2×n(n-1)= n(n-1)对对顶角。
再基于“任意两条直线被第三条直线所截,形成:同位角4对,内错角2对,同旁内角2对”的基本单元构成。
从n条直线中任意选出2条直线,有n(n-1)种可能;剩下(n-2)条直线,这(n-2)条直线就可以作为第三条直线。那么构成上述基本单位的数量为:n(n-1)×(n-2)= n(n-1) (n-2)。
这里“从n条直线中任意选出2条直线,有n(n-1)种可能”是有难度的,属于超范围了,要用到排列组合的相关知识。
基本单元数量有了,所以共形成:
同位角4×n(n-1) (n-2)= 2n(n-1) (n-2)对,内错角2×n(n-1) (n-2)= n(n-1) (n-2)对,同旁内角2×n(n-1) (n-2)= n(n-1) (n-2)对,第二小题完成。
,




