每个数学结论都有其成立的条件,每一种数学方法的使用也往往有其适用范围,在我们所遇到的数学问题中,有些问题的结论不是唯一确定的,有些问题的结论在解题中不能以统一的形式进行研究,还有些问题的已知量是用字母表示数的形式给出的,这样字母的取值不同也会影响问题的解决,由上述几类问题可知,就其解题方法及转化手段而言都是一致的,即把所有研究的问题根据题目的特点和要求,分成若干类,转化成若干个小问题来解决,这种按不同情况分类,然后再逐一研究解决的数学思想,称之为分类讨论思想。
2.分类讨论的基本方法(1)要确定讨论对象以及所讨论对象的全体的范围;
(2)确定分类标准,正确进行合理分类,即标准统一、不漏不重、 再对各个分类逐步进行讨论,分层进行,获取阶段性结果;
(3)进行归纳小结,综合得出结论.
类型1 顶角和底角的分类讨论
方法归纳:对于等腰三角形,只要已知它的一个内角的度数,就能算出其他两个内角的度数,如果题中没有确定这个内角是顶角还是底角,就要分两种情况来讨论.①当这个已知角为顶角时,②当这个已知角为底角时。
针对训练
1.等腰三角形是有一个角为52°,它的一条腰上的高与底边的夹角为多少度?
解:①若已知的这个角为顶角,则底角的度数为(180°-52°)÷2=64°,故一腰上的高与底边的夹角为26°;
②若已知的这个角为底角,则一腰上的高与底边的夹角为38°故所求的一腰上的高与底边的夹角为26°或38°.
类型2 对腰长和底长的分类讨论
方法归纳:在解答已知等腰三角形边长的问题时,当题目条件中没有明确说明哪条边是“腰”,哪条边是“底”时,往往要进行分类讨论.判定的依据是:三角形的任意两边之和大于第三边;两边之差小于第三边.
针对训练
2.若一个等腰三角形的三边长均满足(x-2)(x-4)=0,求此等腰三角形的周长.
解:.据题意,得x=2、x=4都满足(x-2)(x-4)=0.从而可知等腰三角形的三边长有四种可能情况:2、2、4或2、4、4或2、2、2或4、4、4.其中,根据三角形的三边关系知,以2、2、4为边不能构成三角形,而其他三种情况均符合条件.因此,所求等腰三角形的周长为6或10或12.
类型3 对锐角、直角和钝角三角形的分类讨论
方法归纳:根据等腰三角形顶角的大小可以将其分为锐角、直角和钝角三角形.不同的三角形其高、中线、垂直平分线的交点位置均不同,比如锐角三角形腰上的高在这个三角形的内部;直角三角形腰上的高在顶角的顶点上;钝角三角形腰上的高在这个三角形的外部,因此在解答时需要分类讨论.
针对训练
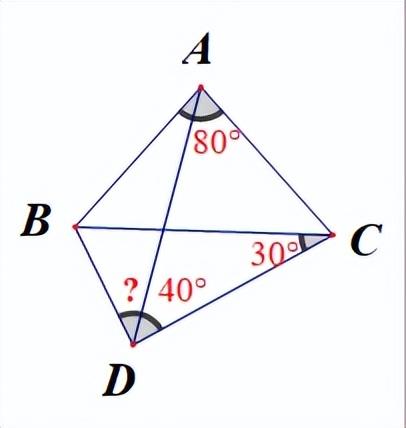
3.AC为等腰△ABD的腰BD上的高,且∠CAB=60°.求这个三角形各内角的度数.
解:.①如图1,高AC在△ABD的内部,因为∠CAB=60°,∠ACB=90°,所以∠B=30°.因为BA=BD,所以∠BAD=∠D=75°;
②如图2,高AC在△ABD的外部,因为∠CAB=60°,∠ACB=90°,所以∠ABC=30°,所以∠ABD=150°.因为BA=BD,所以∠BAD=∠D=15°;
③如图3,高AC在△ABD的外部,因为∠CAB=60°,∠ACB=90°,所以∠B=30°.因为DA=DB,所以∠BAD=∠B=30°,所以∠ADB=120°.www.21-cn-jy.com

类型4 函数中等腰三角形存在性
方法归纳:三角形两个顶点固定,另外一个顶点为动点,简称“两定一动”。此时任何两条边都可能作为腰,因此分三种情况讨论,如在△ABC中,①当点A作为顶点则AB=AC;②当点B作为顶点则BA=BC;③当点C作为顶点则CA=CB.