(三)割补法
在计算一些不规则的几何图形的面积时,把图形中凸出来的部分割下来,填补到相应的凹陷处,或较适当的位置,使图形组合成一个或几个规则的形状,再计算面积的解题方法叫做割补法。
例1:
求图40-13阴影部分的面积。(单位:厘米)(适于六年级程度)

成了一个梯形如图40-14,这个梯形的面积就是图40-13中的阴影部分的面积。
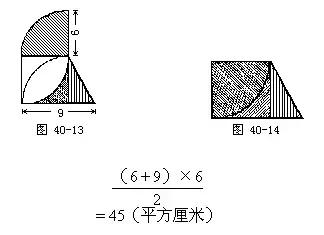
答:阴影部分的面积是45平方厘米。

*例2:
求图40-15中阴影部分的面积。(单位:米)(适于六年级程度)

16×16×2=512(平方米)
答:阴影部分的面积是512平方米。
*例3:
图40-17中,ABCD是正方形,ED=DA=AF=2厘米。求图中阴影部分的面积。(适于六年级程度)
解:经割补,把图40-17组合成图40-18。很容易看出,只要从正方形的面积中减去空白扇形的面积,便得到阴影部分的面积。


答:图中阴影部分的面积是2.43平方厘米。
,




