点击右上角的关注,不定期前端干货分享!!
我的前端图形学系列文章终于迎来了激动人心的时刻,我们要进入物理世界去探索了。主今天的主题,【运动】
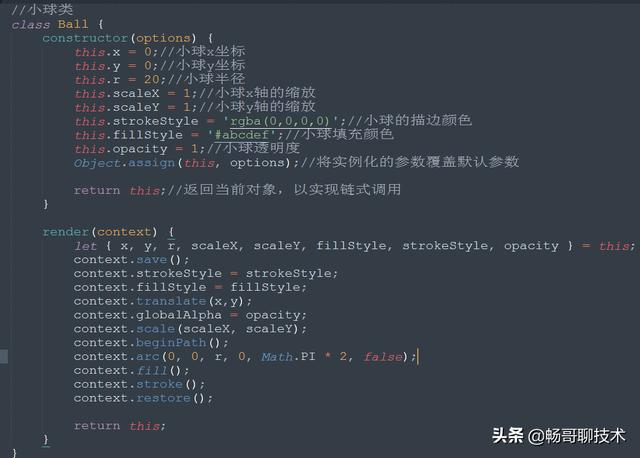
在进入物理世界之前,我们所有的运动都是作用在一个小球身上,所以我们的当务之急就是封装一个小球类,贴代码:
es6类的基础、解构赋值Canvas基础这里就不过多的赘述了
匀速直线运动路程(s) = 时间(t) * 速度(v) 路程随着时间的增加而增加,因为速度恒定。
很简单的公式,这是初中的知识,也很容易理解,那么如果把它应用到前端中,我们来模拟下这个过程。
var canvas = document.querySelector('canvas'); var context = canvas.getContext('2d'); canvas.width = window.innerWidth; canvas.height = window.innerHeight; var {width,height} = canvas; var ball = new Ball({ x:50, y:100 }).render(context); var speed = 1; (function move(){ context.clearRect(0,0,width,height); window.requestAnimationFrame(move); ball.x = speed; ball.render(context); })();
效果:
一个很最最基础的动画就是这样的
这里解释一下:这里我们把路程作用在小球对象的X属性上,speed参数作为速度,因为是匀速运动,所以speed恒定不变,而时间我们则是用requestAnimationFrame来模拟。这样我们就可以把这个最简单的公式应用在我们的图形上了。
正弦曲线运动好吧,又要杠上这骚气的正弦曲线了,接下来我们让小球沿着正弦曲线来运动。效果:
正弦曲线变化的小球
canvas.width = window.innerWidth; canvas.height = window.innerHeight; var {width,height} = canvas; var ball = new Ball({ x:50, y:100, fillStyle:'#f90' }).render(context); var amplitude = 100;//振幅 var vx = 1; var angle = 0; (function move(){ context.clearRect(0,0,width,height); window.requestAnimationFrame(move); ball.x = vx; ball.y = Math.sin(angle) * amplitude 120; angle =0.05; angle%=Math.PI*2; ball.render(context); })();
这里我们实例化了一个小球,然后设置了水平方向的速度vx为1,y轴的速度则为正弦曲线。amplitude为振幅,120为常数,将小球往下平移120。
这里angle为弧度,我们知道正弦曲线的周期是Math.PI*2 所以angle不用大于Math.PI*2
所以我设置了angle %= Math.PI*2
脉冲运动前面两个小的demo,我们都是惯性思维,什么意思呢?就是我们总是想着把速度作用在x,y坐标上,事实上,它可以运用在其它的属性上,可以达到意想不到的效果哦。
接下来要说到的就是脉运动了。先来看效果:
这里我们是将运动属性赋值给了小球的scaleX和scaleY属性上,我们将正弦曲线变换作用在了小球的缩放属性上了,形成了上面的效果,代码如下:
感觉正弦曲线快被我玩儿坏了^_^
总结1、结合初中的简单的物理学公式,映射到了前端图形学的界面开发中,给物理公式公式赋能。
2、当然今天只是前端图形学与物理最简单的结合,后面继续深入物理学与图形学更多美妙的结合,看看物理学和图形学究竟能擦出什么样的火花。
3、正弦曲线灵活运用。
这里是【畅哥聊技术】前端图形学相关技术文章,更多精彩内容敬请关注。未完待续...
,