全等三角形是初中几何的开端,我们需要先掌握基础知识,然后再挑战难题。全等三角形要找准对应关系,对应的顶点、对应的角和对应的边。证明三角形全等至少需要三个条件,其中至少需要一条边。

例题1:如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是:____________.
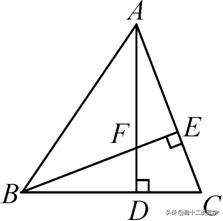
分析:要证明△ADC与△BEC全等,首先两个三角形都是直角三角形,即∠BEC=∠ADC=90°,不要忽视隐含条件,本题中有公共角。当然,也可以利用同角的余角相等或者“8”字形得到∠DAC=∠EBC。两个三角形中已经具备有两组角对应相等,而证明两个三角形全等至少需要一条边。因此,只要添加任意一组边对应相等即可,可以添加AC=BC、BE=AD,通过“AAS”证明两个三角形全等;也可以添加CE=CD,通过“ASA”证明两个三角形全等。
证明三角形全等中常见的隐含条件有:(1)公共边;(2)公共角;(3)对顶角相等;(4)等边加减等边得到等边;(5)等角加减等角等于等角;(6)中点得到线段相等、角平分线得到角度相等;(7)垂直得到两个角相等;(8)等角(同角)的余角相等;(9)等角(同角)的补角相等。

例题2:如图,在Rt△ABC和Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是 ____________.

分析:两个三角形已经具备的条件有:(1)∠A=∠D=90°,(2)BC=CB,已经具备两个条件,两个三角形为直角三角形,如果想利用“HL”定理证明两个三角形全等,那么可以添加AB=DC或AC=BD。如果想利用“AAS”证明两个三角形全等,那么可以添加∠A=∠D或∠ABC=∠DCB。
解答此题的关键是要明确:①判定定理1:SSS--三条边分别对应相等的两个三角形全等.②判定定理2:SAS--两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA--两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS--两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL--斜边与直角边对应相等的两个直角三角形全等。
判断两个直角三角形全等时,不能只想到“HL”定理,其它几个定理都可以证明两个直角三角形全等。

例题3:如图,AB平分∠DAC,BD=BC,△ADB与△BCA全等吗?说明理由.

分析:已知AB平分∠DAC,那么得到∠DAB=∠CAB,公共边AB=AB,还有边BD=BC,“SSA”无法证明两个三角形全等,因此两个三角形不全等。
不能准确找出判定三角形全等的条件,易盲目地运用三角形全等的条件“强行”判定两个三角形全等。
,




