在解答几何题中，有时候题目和图形都很简单，往往要去构造新的图形才能将条件串联起来，这时候就要学会用到特殊角和特殊图形的特点。看下面这道中考题。

题目：如图，在△ABC中，∠BAC=120°，AB=5，AC=7.5，∠BAC的平分线与BC交于点D，求线段AD的长度。

构造直角三角形解题技巧（一种常见但有效的解题思路）(1)

一般经过类似题目训练的朋友，看到题目中∠BAC=120°，就会想到60°角，就会想着去构造正三角形来解题，这个思路是对的。请看图：

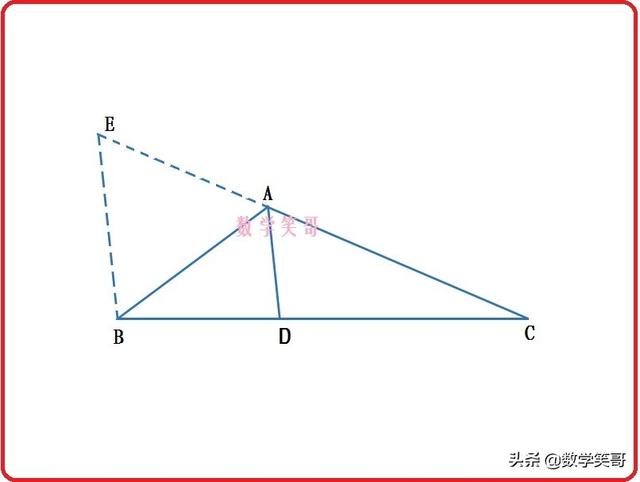
构造直角三角形解题技巧（一种常见但有效的解题思路）(2)

解：

做CA延长线到E点，使AE=AB，连接BE。

∵∠BAC=120°，∴∠BAE=60°，

又∵AB=AE，∴△ABE为正三角形，AE=BE=AB=5，

∴CE=AC AE=12.5。

∵∠BAC=120°，AD为∠BAC的平分线，∴∠CAD=60°，

又∴△ABE为正三角形，∴∠AEB=60°，

∴AD∥EB。

∴在大△BCE中，△DAC∽△BCE，

∴，

∴。

经验：

通过解答类似题目，我们只要看到120°角或者135°角，都要想着构造正三角形或者等腰直角三角形，来试试能不能快速找到解题思路。

多谢大家阅读，多谢点赞关注支持。[送心][送心][送心][送心][送心]

,