一道初中题-求小圆的半径
在下图中,一段圆弧的圆心在正方形的一个顶点上,正方形的边长为3,且这段圆弧经过正方形的另外两个顶点。有一个小圆即和大圆,也和正方形的两条边相切。 求这个小圆的半径。

解:这里给出两个解法
方法1.
如图中的大直角三角形, 一个斜边为4 r, 两条直角边各是4-r,
可以利用勾股定理,或者用45-45-90度的直角三角形的边的关系。
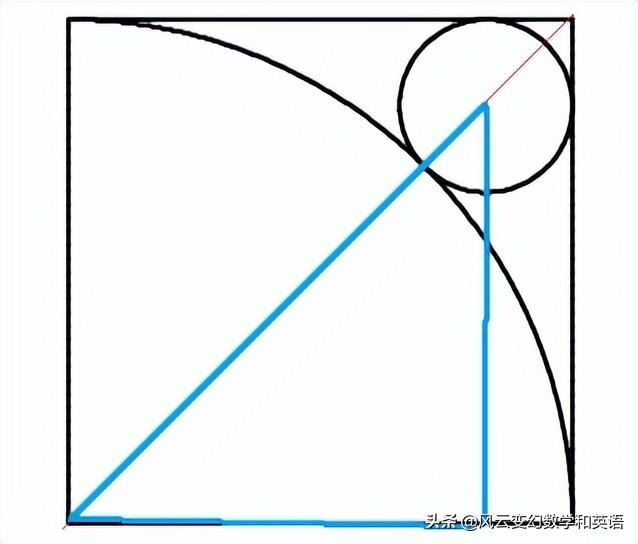
我们利用45-45-90度的等腰三角形的变的关系:
4 r=√2(4-r)
由此得出r=12-8√2
方法2:利用右上方顶角的等腰直角三角形

这个小的直角三角形的斜边为4√2-4-r, 而两条直角边都是r,
根据45-45-90度的直角三角形的边长的关系有:
4√2-4-r=√2r
解这个方程得出:
r=12-8√2
总结:对于初中的学生,若要解直角三角形,有两种方法
- 勾股定理的应用,特别是几种特殊形式的,如3-4-5, 5-12-13等。
- 特殊角的直角三角形,如30-60-90度,和本题的45-45-90度。





