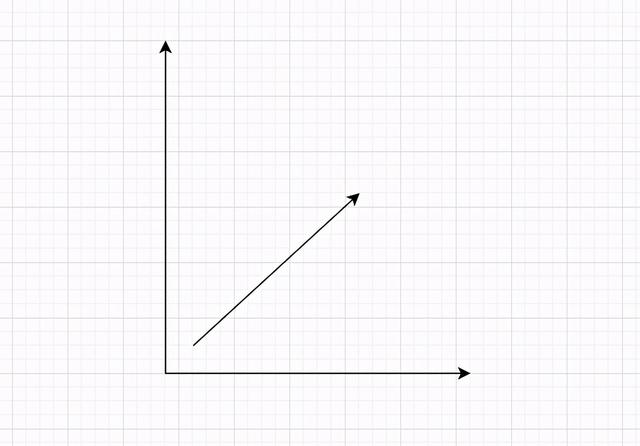
指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段;箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
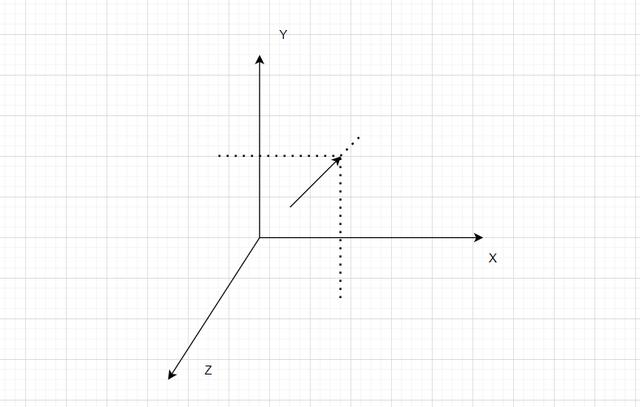
- 直角坐标系也叫笛卡尔坐标系
- 原本的二维坐标系(x,y 轴),再增加一个垂直的 z 轴
- z 轴方向不同分成右手系和左手系

三维空间向量
- 二维
第一种是通常向量的表示,应该在数字的上方带一个箭头,用来区分向量,第二种是通过矩阵来表示,第三种是单位向量来表示。

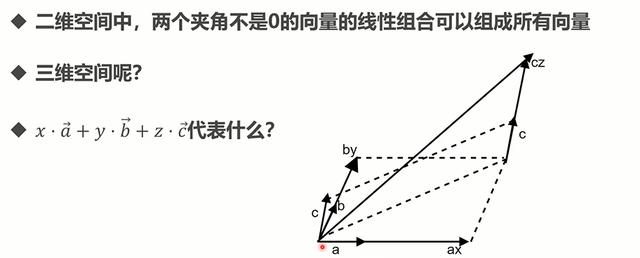
- 三维
可以组合三维中任意向量
- 向量乘以常数:向量乘以常数可以看到向量被成倍延长了;负数倍数会返过来:


- 二维
前提是两个向量不是平行的。

- 三维
可以组合三维中任意向量


由极点(pole)和射线(ray)组成的坐标系。用(角度,射线长度)描述一个点 比如图中的(3, 60°)表示射线长3,从 0L 转动 60 度。

由极点和射线构成极坐标系中点:




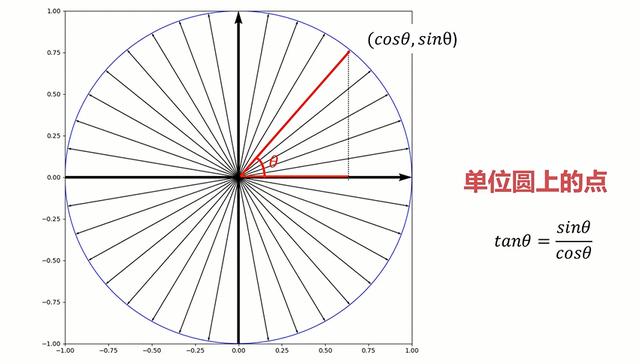
三角函数运算
- cos(a b) = cc - ss
- sin(a b) = cs sc

向量积也叫叉积,外积,它也是向量与向量的乘积,不过需要注意的是,它的结果是个向量。它的几何意义是所得的向量与被乘向量所在平面垂直,方向由右手定则规定,大小是两个被乘向量张成的平行四边形的面积。

向量积可以被定义为:
模长:(在这里 θ 表示两向量之间的夹角(共起点的前提下)(0°≤θ≤180°),它位于这两个矢量所定义的平面上。)
方向:a 向量与 b 向量的向量积的方向与这两个向量所在平面垂直,且遵守右手定则。
也可以这样定义(等效):向量积 |c|=|a×b|=|a||b|sin<a,b> 即 c 的长度在数值上等于以 a,b,夹角为 θ 组成的平行四边形的面积。而 c 的方向垂直于 a 与 b 所决定的平面,c 的指向按右手定则从 a 转向 b 来确定。
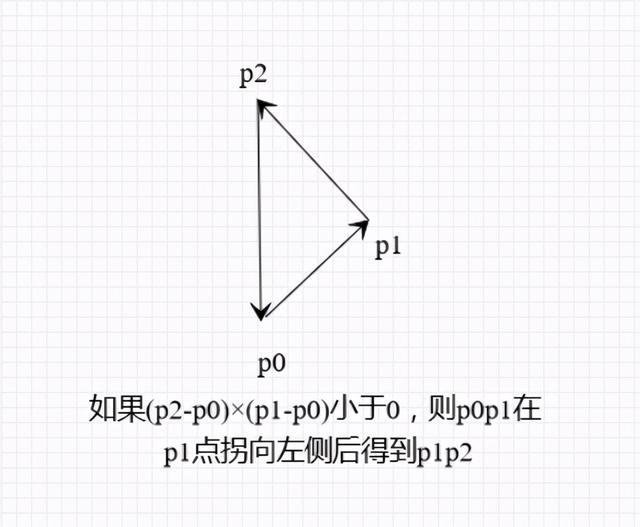
计算矢量叉积是与直线和线段相关算法的核心部分。设矢量 P = (x1, y1),Q = (x2, y2),则矢量叉积定义为由(0, 0)、P1、P2 和 P1P2 所组成的平行四边形的带符号的面积, 即:P × Q = x1.y2 - y2.y1,其结果是一个标量,显然有性质 P × Q = -(Q × P) 和 P × (-Q) = -(P × Q)
向量外积的几何意义:
- 在三维几何中,向量 P 和向量 Q 的外积结果是一个向量,有个更通俗易懂的叫法是法向量,该向量垂直于 P 和 Q 向量构成的平面。
- 在 3D 图像学中,外积的概念非常有用,可以通过两个向量的外积,生成第三个垂直于 P,Q 的法向量,从而构建 X、Y、Z 坐标系。
- 在二维空间中,外积还有另外一个几何意义就是:|a×b| 在数值上等于由向量 P 和向量 Q 构成的平行四边形的面积。


- 向量叉乘指向向量 a 和 b 的垂直方向
- 值等于 a 和 b 形成的平行四边形面积
- a、b 和 c 的叉乘是 a、b、c 形成的平行六面体体积





