类型1 一般的猜想探究题
一般几何题的猜想与证明近几年在中考中间断性出现,以学生探究为主线,置身于数学问题的发现与解决中,一般在最后3题中一题,以综合与实践的形式出现,考查学生分析问题、解决问题的能力.常综合平行线、等腰三角形(等边三角形)、直角三角形、平行四边形、矩形、正方形等知识为一体,借助逻辑推理一步一步证明,建立方程模型思想,如常见的通过勾股定理、相似三角形对应边成比例、解直角三角形、面积法、平行线分线段成比例定理等得出关于未知数的方程,从而求解.

例1.(2018山西) 综合与实践
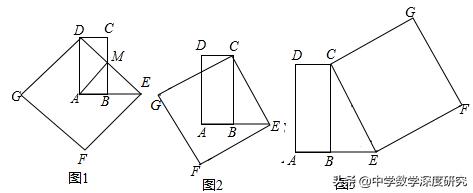
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM,试判断线段AM与DE的位置关系。
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵ BE=AB, ∴ AE=2AB.
∵ AD=2AB,∴ AD=AE
∵ 四边形ABCD是矩形, ∴ AD∥BC
∴ EM/DM=EB/AB . (依据1)
∵ BE=AB,∴EM/DM=1. ∴EM=DM
即AM是△ADE的DE边上的中线,
又∵ AD=AE,∴ AM⊥DE . (依据2)
∴ AM垂直平分DE.
反思交流:
(1) ①上述证明过程中的"依据1""依据2"分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
(2) 创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3) 如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形GEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明。
【思路分析】本题考查了矩形及垂直平分线的性质,解题的关键是作辅助线构造全等三角形进行解答.(1)依据1是由平行得到比例的关系;依据2是等腰三角形的性质,由中线得到垂直;(2)过点G作GH⊥BC于点H,利用AAS证明△GHC≌△CBE,则CH=BE,结合已知条件AD=2AB, BE=AB,结论可证;(3)与(2)的证明方法相似,过点F作FM⊥BC于点M,过点E作EN⊥FM于点N,可证△ENF≌△EBC,结合已知条件,结论可证.
【解答过程】(1)①依据1:两条直线被一组平行线所截,所得的对应线段成比例(或平行线分线段成比例)。
依据2:等腰三角形顶角的平分线,底边上的中线及底边上的高互相重合(或等腰三角形的"三线合一")
(2)证明:过点G作GH⊥BC于点H,

∵ 四边形ABCD是矩形,点E在AB的延长线上,
∴ ∠CBE=∠ABC=∠GHC=90° .∴ ∠BCE ∠BEC=90°
∵ 四边形CEFG为正方形,∴ CG=CE,∠GCE=90°.
∴ ∠GCB ∠BCE=90°. ∴ ∠BEC=∠GCB.
∴ △GHC≌△CBE. ∴ HC=BE.
∵ 四边形ABCD是矩形,∴ AD=BC
∵ AD=2AB, BE=AB,∴ BC=2BE=2HC.
∴ HC= BH,∴ GH垂直平分BC.
∴ 点G在BC的垂直平分线上
(3)答:点F在BC边的垂直平分线上(或点F在AD边的垂直平分线上).
证明:过点F作FM⊥BC于点M,过点E作EN⊥FM于点N

∴ ∠BMN=∠ENM=∠ENF=90°.
∵ 四边形ABCD是矩形,点E在AB的延长线
∴ ∠CBE=∠ABC=90°,∴ 四边形BENM为矩形
∴ BM=EN, ∠BEN=90°,∴ ∠1 ∠2=90°
∵ 四边形CEFG为正方形,∴ EF=EC,∠CEF=90°
∴ ∠2 ∠3=90°,∴ ∠1=∠3
∵ ∠CBE=∠ENF=90°,∴ △ENF≌△EBC.
∴ NE=BE.∴ BM=BE.
∵ 四边形ABCD是矩形,∴ AD=BC
∵ AD=2AB,AB=BE,∴ BC=2BM,∴ BM=MC
∴ FM垂直平分BC,∴ 点F在BC边的垂直平分线上.

【一题多解】(3)方法二:过F作FN⊥BE交BE的延长线于点N,连接FB,FC.

∵四边形ABCD是矩形,点E在AB的延长线上.
∴∠CBE=∠ABC=∠N=90°. ∴∠BEC ∠BCE=90°.
∵四边形CEFG为正方形,∴EC=EF,∠CEF=90°.
∴∠BEC ∠FEN=90°.∴∠FEN=∠BCE.∴△ENF≌△CBE.
∴NF=BE,NE=BC.
∵四边形ABCD是矩形,∴AD=BC.
∵AD=2AB,BE=AB.∴设BE=a,则BC=EN=2a,NF=a.

∴BF=CF.∴点F在BC边的垂直平分线上.
方法规律:在复习一般几何题的猜想探究题目时,要注意证明推理和方程模型计算的综合,要对条件进行合理猜想与推理,结合自己的解题经验及对题目的把握灵活处理.复习时注意以下几点:
1、注意总结考查知识的面与点,了解此类题目的特点;
2、针对此类问题的练习要注意总结知识间的联系,提升思维的开放性;3、针对自己在做题中遇到的问题进行相应的总结与练习,不断提升分析问题、解决问题的能力.

类型2 图形平移型
图形平移的探究题近几年在中考中间断性出现,主要以探究为主线,令学生置身于数学问题的发现与解决中, 一般在最后3题中一题,以综合与实践、23题结合函数以压轴题的形式出现,考查学生分析问题和解决问题的能力.常综合平行线、等腰三角形(等边三角形)、直角三角形、平行四边形、矩形、正方形等知识为一体,借助逻辑推理一步一步证明,建立方程模型思想,如常见的通过勾股定理、相似三角形对应边成比例、解直角三角形、面积法、平行线分线段成比例定理等得出关于未知数的方程,从而求解.
例2.(2018·贵港)已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持∠ABP=90°,BP边与直线l相交于点P.
(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;
(2)请利用如图1所示的情形,求证:AB/PB=OM/BM ;
(3)若AO=2√6 ,且MO=2PO,请直接写出AB和PB的长.

【思路分析】(1)先证明四边形OCBM是平行四边形,再由∠BMO=90°,得出▱OCBM是矩形,最后根据直角三角形斜边上的中线的性质即可证明四边形OCBM是正方形.
(2)连接AP、OB,由于∠ABP=∠AOP=90°,所以A、B、O、P四点共圆,从而利用圆周角定理可证明∠APB=∠OBM,所以△APB∽△OBM,利用相似三角形的性质即可求出答案.
(3)由于点P的位置不确定,故需要分情况进行讨论,共两种情况,第一种情况是点P在O的左侧时,第二种情况是点P在O的右侧时,然后利用四点共圆、相似三角形的判定与性质、勾股定理即可求出答案.

【解答过程】 (1)∵2BM=AO,2CO=AO,∴BM=CO,
∵AO∥BM,∴四边形OCBM是平行四边形,
∵∠BMO=90°,∴▱OCBM是矩形,
∵∠ABP=90°,C是AO的中点,
∴OC=BC,∴矩形OCBM是正方形.

(2)如图,连接AP、OB,
∵∠ABP=∠AOP=90°,∴A、B、O、P四点共圆,
由圆周角定理可知∠APB=∠AOB,
∵AO∥BM,∴∠AOB=∠OBM,∴∠APB=∠OBM,
∴△APB∽△OBM,∴AB/PB=OM/BM
(3)当点P在O的左侧时,如图所示,过点B作BD⊥AO于点D,

易证△PEO∽△BED,∴PO/BD=OE/DE,易证:四边形DBMO是矩形,
∴BD=MO,OD=BM,∴MO=2PO=BD,∴OE/DE=1/2,
∵AO=2BM=2√6,∴BM=√6,∴OE=√6/3,DE=2√6/3,
易证△ADB∽△ABE,∴AB²=AD•AE,
∵AD=DO=BM=√6,∴AE=AD DE=5√6/3,∴AB=√10,
由勾股定理可知:BE=2√15/3,易证:△PEO∽△PBM,
∴BE/FB=OM/PM=2/3,∴PB=√15,
当点P在O的右侧时,如图所示,
过点B作BD⊥OA于点D,
∵MO=2PO,∴点P是OM的中点,
设PM=x,BD=2x,
∵∠AOM=∠ABP=90°,∴A、O、P、B四点共圆,
∴四边形AOPB是圆内接四边形,∴∠BPM=∠A,∴△ABD∽△PBM,
∴AD/BD=PM/BM,
又易证四边形ODBM是矩形,AO=2BM,
∴AD=BM=√6,∴√6/2x=x/6,解得:x=√3,∴BD=2x=2√3,
由勾股定理可知:AB=3√2,PB=3,
综上所述,AB=√10,PB=√15或AB=3√2,PB=3.
方法规律:平移不改变图形的大小和形状,对应线段相等,对应角相等.综合复习时要注意证明推理和方程模型计算的综合,要对条件进行合理猜想与推理,结合自己的解题经验及对题目的把握灵活处理.复习时注意以下几点:1、注意总结考查知识的面与点,了解此类题目的特点;2、针对此类问题的练习要注意总结知识间的联系,提升思维的开放性;3、针对自己在做题中遇到的问题进行相应的总结与练习,不断提升分析问题和解决问题的能力.

类型3 图形旋转型
图形的旋转型探究题近几年在中考中间断性出现,主要以探究为主线,令学生置身于数学的问题发现与解决中, 一般在最后3题中一题,以综合与实践、结合函数以压轴题的形式出现,考查学生分析问题和解决问题的能力.常综合平行线、等腰三角形(等边三角形)、直角三角形、平行四边形、矩形、正方形等知识为一体,借助逻辑推理一步一步证明,建立方程模型思想,如常见的通过勾股定理、相似三角形对应边成比例、解直角三角形、面积法、平行线分线段成比例定理等得出关于未知数的方程,从而求解.
例3.(2018山东烟台中考题)
【问题解决】
一节数学课上,老师提出了一个这样问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3,你能求出∠APB的度数吗?
小明他通过观察、分析、思考,形成了如下思路:
思路一:将△PBC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP′B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
【类比探究】
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=√11,求∠APB的度数.

【思路分析】(1)如图(1)将△PBC绕点B逆时针旋转90°得到△BP′A,连接PP′,得到等腰直角三角形△BP′P,从而得到PP′=2√2,∠BPP′=45°,又AP′=CP=3,AP=1,
∴AP² P′P²=1 8=9= P′A²,∴根据勾股定理逆定理得∠APP′=90°,从而求出∠APB=45°+90°=135°;(2)如图(2)将△PBC绕点B逆时针旋转90°,得到△BP′A,连接PP′,方法和(1)类似,求出∠APB=45°.
【解答过程】(1)如图(1)将△PBC绕点B逆时针旋转90°,得到△BP′A,连接PP′,
∵PB=P′B=2,∠P′BP=90°,
∴PP′=2√2,∠BPP′=45°.
又AP′=CP=3,AP=1,
∴AP² P′P²=1 8=9= P′A²,
∴∠APP′=90°,∴∠APB=45°+90°=135°.
(2)如图(2)将△PBC绕点B逆时针旋转90°,得到△BP′A,连接PP′,
∵PB=P′B=1,∠P′BP=90°,
∴PP′=√2,∠BPP′=45°.
又AP′=CP=√11,AP=3,
∴AP² P′P²=9 2=11= P′A²,
∴∠APP′=90°,∴∠APB=90°-45°=45°.

方法规律:旋转不改变图形的大小和形状,对应线段相等,对应角相等;对应点的连线与旋转中心的夹角叫旋转角.综合复习时要注意证明推理和方程模型计算的综合,要对条件进行合理猜想与推理,结合自己的解题经验及对题目的把握灵活处理.
阅读材料问题往往会提供一些解题方法或给出解题暗示,要求在理解的基础上再进行问题的解答,或在阅读材料中提供一些操作方法,要求同学们去模拟并探究,或提供一个解题过程,这种题不仅考查了同学们的阅读能力,而且还综合考查了同学们的创新意识及转化能力.

类型4 图形折叠型
图形的折叠探究题近几年在中考中间断性出现,主要以操作探究为主,令学生置身于数学的问题发现与解决中, 一般在最后3题中一题,以综合与实践出现,考查学生分析问题和解决问题的能力.常综合平行线、等腰三角形(等边三角形)、直角三角形、平行四边形、矩形、正方形等知识为一体,借助逻辑推理一步一步证明,建立方程模型思想,如常见的通过勾股定理、相似三角形对应边成比例、解直角三角形、面积法、平行线分线段成比例定理等得出关于未知数的方程,从而求解.
例4.(2018云南昆明中考题)如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°,将△ADP沿AP翻折得到△AD'P, P D'的延长线交AB边于点M,过点B作BN∥MP交DC于点N.
(1)求证:AD²=DP·PC;
(2)判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若DP/AD=1/2,求EF/AE的值.

【思路分析】本题考查相似三角形的综合问题,涉及相似三角形的性质与判定,菱形的判定,直角三角形斜边上的中线的性质等知识,综合程度较高,需要学生灵活运用所学知识.
(1)根据四边形ABCD是矩形,可证得AD=BC,然后证明∠DAP=∠BPC,即可证得△ADP∽△PCB;(2)先证明四边形PMBN是平行四边形,然后由△ADP沿AP翻折得到△AD'P,可证得∠APM=∠PAM,再根据∠APB=90°,可证明∠PBA=∠BPM,即可得证;(3)设DP=a,可根据DP/AD=1/2,AD²=DP·PC,求得PC=4 a,AB=5a,PM=BM=5a/2,然后证明△CFP∽△AFB,求得CF/AC的值,再证明△AEM∽△CEP,求出EF/AC的值,从而求出EF/AE的值.
【解答过程】(1)证明:∵四边形ABCD是矩形,∴AD=BC,∠D=∠BCD=90°,又∵∠APB=90°,∴∠DAP+∠APD=90°,∠APD+∠BPC=90°,∴∠DAP=∠BPC,又∵∠D=∠BCP=90°,∴△ADP∽△PCB,∴AD/PC=DP/CB,又∵AD=BC,∴AD/PC=DP/AD,AD²=DP·PC;
(2)∵四边形ABCD是矩形,∴AB∥DC,即PN∥BM,又∵BN∥MP,∴四边形PMBN是平行四边形,∵△ADP沿AP翻折得到△AD'P,∴∠APD=∠AP D',又∵AB∥DC,∴∠APD=∠APM=∠PAM,又∵∠APB=90°,∴∠APM+∠PBA=90°,∠APM+∠BPM=90°,∴∠PBA=∠BPM,∴PM=BM,∴平行四边形PMBN是菱形;
(3)设DP=a,∵DP/AD=1/2,∴AD=2DP=2 a,又∵AD²=DP·PC,∴(2 a)²=a·PC,解得PC=4 a,∴AB=CD=DP+PC=5a,又∵PM=BM,∴PM=BM=5a/2,∵AB∥DC,∴∠CPF=∠ABF,又∵∠PFC=∠BFA,∴△CFP∽△AFB,∴CF/AF=CP/AB=4a/5a=4/5,∴CF/AC=5/(5 4)=5/9,∵AB∥DC,∴∠CPE=∠AME,又∵∠PEC=∠MEA,∴△AEM∽△CEP,

【易错点睛】此类问题容易出错的地方是第2问看图形只能得到平行四边形,没有进一步思考,第3问用2次相似,不太容易想到

【方法规律】(1)从要证明的式子AD2=DP·PC来看,很容易想到相似;(2)从题中条件可以先证明平行四边形,再有直角的条件,就可以证明角平分线,不难证明菱形(3)设DP=a,再想办法把其他能用参数a表示的边都表示出来,把要求的线段的比表示出来。
折叠前后,图形的大小和形状不变,对应线段相等,对应角相等.综合复习时要注意证明推理和方程模型计算的综合,要对条件进行合理猜想与推理,结合自己的解题经验及对题目的把握灵活处理.
(配套练习可私信与我,留下信箱,会及时发送)
,