一、频率分布
1、频率分布的意义
在许多问题中,只知道平均数和方差还不够,还需要知道样本中数据在各个小范围所占的比例的大小,这就需要研究如何对一组数据进行整理,以便得到它的频率分布。
2、研究频率分布的一般步骤及有关概念
(1)研究样本的频率分布的一般步骤是:
①计算极差(最大值与最小值的差)
②决定组距与组数
③决定分点
④列频率分布表
⑤画频率分布直方图
(2)频率分布的有关概念
①极差:最大值与最小值的差
②频数:落在各个小组内的数据的个数
③频率:每一小组的频数与数据总数(样本容量n)的比值叫做这一小组的频率。
二、确定事件和随机事件
1、确定事件
必然发生的事件:在一定的条件下重复进行试验时,在每次试验中必然会
发生的事件。
不可能发生的事件:有的事件在每次试验中都不会发生,这样的事件叫做不可能的事件。
2、随机事件:
在一定条件下,可能发生也可能不放声的事件,称为随机事件。
3、随机事件发生的可能性
一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同。
对随机事件发生的可能性的大小,我们利用反复试验所获取一定的经验数据可以预测它们发生机会的大小。要评判一些游戏规则对参与游戏者是否公平,就是看它们发生的可能性是否一样。所谓判断事件可能性是否相同,就是要看各事件发生的可能性的大小是否一样,用数据来说明问题。
三、概率
1、概率的意义 一般地,在大量重复试验中,如果事件A发生的频率
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率。
2、事件和概率的表示方法
一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P
四、确定事件和随机事件的概率之间的关系
1、确定事件概率
(1)当A是必然发生的事件时,P(A)=1
(2)当A是不可能发生的事件时,P(A)=0
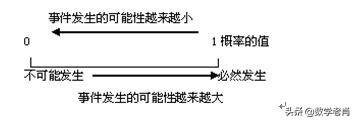
2、确定事件和随机事件的概率之间的关系
五、古典概型
1、古典概型的定义
某个试验若具有:①在一次试验中,可能出现的结构有有限多个;②在一次试验中,各种结果发生的可能性相等。我们把具有这两个特点的试验称为古典概型。
2、古典概型的概率的求法
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=
(1)、列表法
用列出表格的方法来分析和求解某些事件的概率的方法叫做列表法。
(2)、树状图法
就是通过列树状图列出某事件的所有可能的结
果,求出其概率的方法叫做树状图法。
六、利用频率估计概率
1、利用频率估计概率
在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率。
2、在统计学中,常用较为简单的试验方法代替实际操作中复杂的试验来完成概率估计,这样的试验称为模拟实验。
3、随机数
在随机事件中,需要用大量重复试验产生一串随机的数据来开展统计工作。把这些随机产生的数据称为随机数。
,




