在立体几何中,点、线、面之间的位置关系,特别是线面、面面的平行和垂直关系,是高中立体几何的理论基础,是高考中命题的热点与重点之一。下面就近几年新课标高考立体几何试题中线面、面面的平行与垂直关系进行系统总结,供同学们参考学习!
一. 直线与平面平行的判定1.直线和平面平行的定义:如果一条直线和一个平面没有公共点,那么这条直线和这个平面平行。
2.直线和平面平行的判定定理:如果平面外的一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
3.两个平面平行的性质定理:如果两个平面相互平行,那么在其中一个平面内的直线必平行于另一个平面。
4.利用共面向量定理,先在平面a 内取两个不共线的非零向量e1 ,e2 ,若直线L的方向向量为a,则直线L平行a的条件是存在一组实数对x、y ,使得a=x e1 y e 2。

1.直线和平面垂直的定义:一条直线和 一个平面内的任何一条直线都垂直,则这条 直线和这个平面垂直。
2.直线和平面垂直的判定定理:如果一 条直线和一个平面内的两条相交直线都垂 直,那么这条直线和这个平面垂直。
3.平面与平面平行的性质定理:如果一 条直线垂直于两个平行平面中的一个平面那么它也垂直于另一个平面。
4.平面与平面垂直的性质定理:如果两 个平面垂直,那么在一个平面内垂直于它们 的交线的直线垂直于另一个平面。
5.引入向量,先找出直线的方向向量和 平面的法向量,然后证明这个方向向量和法向量相互平行即可。

1 、两个平面相互垂直的定义:如果两个 相交平面所成的二面角是直二面角,那么这 两个平面相互垂直。
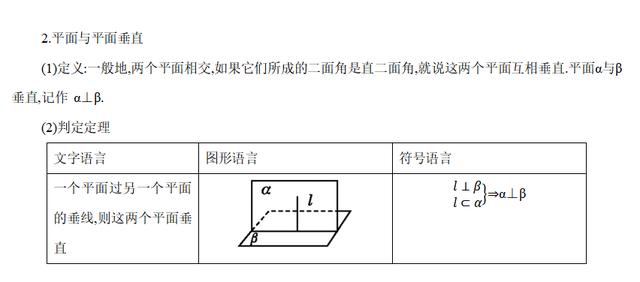
2. 两个平面相互垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面相互垂直。
3. 引入向量,找出两个平面的法向量,然 后证明这两个法向量相互垂直即可。