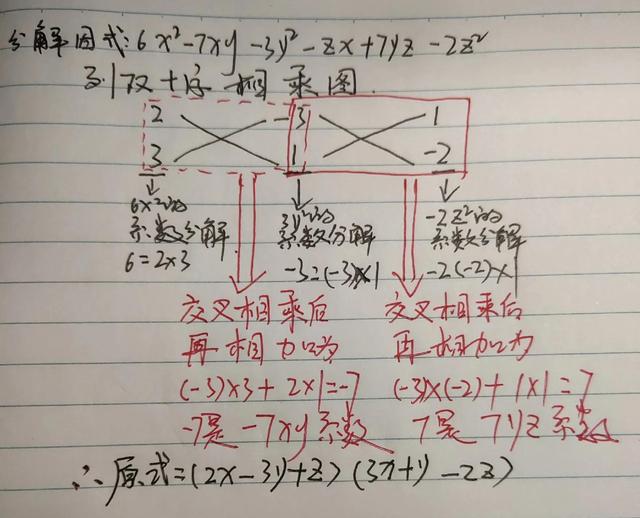
对多项式S分解因式:

我们先回顾一下相关知识:
一、定义
把一个多项式在一个范围化为几个整式的积的形式,这种式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式。
因式分解是中学数学中最重要的恒等变形之一,它被广泛地应用于初等数学之中,在数学求根作图、解一元二次方程方面也有很广泛的应用,是解决许多数学问题的有力工具。
二、方法
因式分解主要有十字相乘法,待定系数法,双十字相乘法,对称多项式,轮换对称多项式法,余式定理法等方法,求根公因式分解没有普遍适用的方法,初中数学教材中主要介绍了提公因式法、运用公式法、分组分解法。而在竞赛上,又有拆项和添减项法式法,换元法,长除法,短除法,除法等。
三、基本步骤:
(1)找出公因式;
(2)提公因式并确定另一个因式;
四、口诀:
口诀:找准公因式,一次要提尽,全家都搬走,留1把家守,提负要变号,变形看奇偶。
我们回到题目:

第一步,分析
题目中S包含有多项式的平方,和三次项,如果直接开平方出来的话,将产生六次项,分解难度增大,计算量将无法估计不是好办法。考虑平方就会联想到平方差公式,考虑立方就会联想到立方差和立方和公式,分解后,预计会产生公因子,按此思路我们进行配系数,得到:

按平方差公式分解因式,按立方差分解因式,都是基本公式,没有难度,直接写出代数式即可:

整理化简后,得到:

发现,确实存在公因子,可以提取公因子,提取公因子后得到:
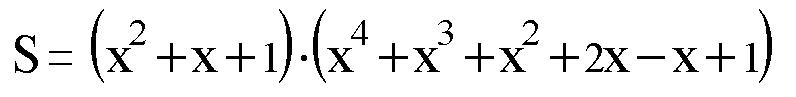
整理化简后得到:

两个乘积项在实数范围内已经不能再因式分解了,上式即为最终答案。
,