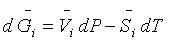提示:本文极长,详细的讲解了计算自由能校正的原理和一些注意事项,内容非常的多,建议耐心看完。如果只关心如何算,可以直接跳到本文看3-5节相应内容即可。
自由能与热力学量校正计算-
1、前言
-
2、计算原理
-
2.1 配分函数*Q*
-
2.2 配分函数和热力学量
-
2.3 分子配分函数*q*
-
3、实际案例分析
-
3.1 计算各配分函数贡献
-
3.2 计算分子自由能校正
-
3.3 误差在哪
-
4、VASPKIT做自由能校正操作
-
4.1 气体分子自由能校正
-
4.2 液体分子自由能校正
-
4.3 吸附分子自由能校正
-
4.4 固体自由能校正
-
5 查JANAF-NIST表计算气体分子的自由能校正
1、前言
理论计算催化中的反应自由能变化是最为重要的内容之一,但是主流第一性原理计算程序VASP没有内置直接计算分子自由能的模块(注: 计算化学程序如Gaussian,CP2K有自由能计算模块)。导致大量VASP计算催化文献中的自由能校正方法不统一,不准确,甚至出现严重的定量错误。比如著名的ORR(oxygen reduction reaction, O2 2H2-> 2H2O, 标况下G = - 4.92 eV),NRR(Nitrogen reduction reaction, 2N2 3H2-> 2NH3,标况下G = - 0.34 eV)反应。(注:实验热力学数据在JANAF-NIST)
无论是气相化学反应,还是表面、材料的化学变化,都是在一定反应条件下进行的,但是直接用第一性原理程序计算出来的都是指0K下忽略零点振动能(ZPE)的能量(俗称电子能量)。自由能校正中首先要校正的就是ZPE,然后计算配分函数,校正体系内能(U)、焓(H)、熵(S)等,由此可以引入反应温度、分压对能量的影响,最后可以进一步考虑 pH、电极电势等等其他外界因素对能量的影响,讨论结果才和真实的实验情况更为接近。
做自由能校正对于催化反应过程的分析有重要意义。比如下图中的对合成氨反应在不同的温度和压强下做自由能变化图:(a)温度升高(300 K -> 700 K,1 bar),总反应的自由能从放热过程(自发)变为吸热过程(非自发)。(b)压强增大(1 bar -> 100 bar, 700 K),总反应的自由能从吸热过程变为放热过程。
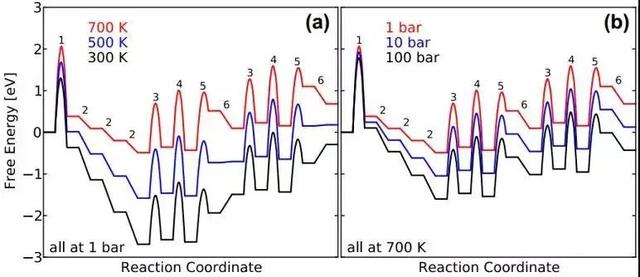
虽然本文主要讲解表面和固体方向的第一性原理计算,但是和表面相关的计算经常涉及到分子的吸附、脱附过程,这必然要涉及到要计算分子、溶液、表面、固体等多体系的自由能计算。本章从孤立分子的自由能校正讲起,再延申到吸附分子、溶液分子,最后讲解固体的自由能计算。
2、计算原理
这一章涉及比较多的统计力学知识,不关心的同学可以跳过,直接看怎么算就行了。这些都写到程序里了,可以当成黑盒子用。VASPKIT可以非常轻松的校正气体分子和吸附分子的自由能,采用的计算原理和 Gaussian程序完全一样,也比较验证过计算结果完全一样。对计算校正原理感兴趣的朋友可以看看高斯的网站:https://gaussian.com/thermo/
2.1 配分函数Q
统计热力学中最关键的量是配分函数Q,
Q物理意义是体系的平均热可及的量子态数,由它可以得到各种热力学性质。但是微观体系计算中只能得到单个分子的性质,所以就需要把系综的配分函数和分子的配分函数联系起来。含N个分子的系综的配分函数Q与单个分子的配分函数q之间有如下关系,即系综的配分函数Q= 分子配分函数的连乘积 除 不可分辨系数N!:
那么这个公式是怎么的出来的呢?其实它是基于理想气体假设的,密度极小的气体分子之间的相互作用可以忽略,则其总内能可以近似表达成所有的N个分子所处能级的能量之和:
为单个气体分子i所处能级能量。带入到配分函数Q的表达式,正则配分函数Q则可以改写成:
其中是单个分子所有可能的能级集合。这个表达式的连乘和求和可以互换,如果分子是全同的,即可写成:
其中分子配分函数即是单个分子所有可能的能级的加权之和:
对于同种分子组成的理想气体,由于微观粒子内禀不可分辨特征,需要加入全同修正1/N!,即得:
2.2 配分函数和热力学量
有了配分函数,就用来求解相应的宏观热力学量了,这里推荐阅读McQuarrie, §7-6一书中的详细讲解。比如体系的内能(U)可以表达成:
亥姆霍兹自由能(A)可以表达成:,根据,体系的熵(S)可以表达成:
又因为体系吉布斯自由能,焓,可以进一步求出体系的吉布斯自由能G和焓H。体系的等容热容(Cv)等压热容(Cp)又可以分别写成内能和焓对温度的偏导数,,。实际上,体系从0K升温到T K所产生的内能和焓的变化又可以写成热容的积分:
在部分文献中可以看到热容校正就是指的这一项。
2.3 分子配分函数q
分子配分函数是将有大量分子的系统中微观物理状态(例如:动能、势能)与宏观物理量统计规律 (例如:压力、体积、温度、热力学函数、状态方程等)连结起来的科学。如气体分子系统中的压力、体积、温度。一个分子的能量可以认为是由分子的整体运动的能量(平动能),以及分子内部运动的能量(转动能,振动能,电子激发能)之和,注意:各种自由度之间是可以耦合的,比如振转耦合,非绝热耦合等。
因此,q可以改写成:
从2.2节中我们已经观察到,配分函数在这些热力学量的表达式中总是以对数ln(Q)的形式出现的,所以我们就需要在对数项中把不同配分函数的贡献拆解开来:
(1)电子激发分子配分函数:
如果基态和激发态的能量差远大于kT,则其激发态的贡献相比于基态就可以忽略。室温(298 K)下kT= 0.0257 eV,而电子激发态的能量一般要远高于基态,所以这一项仅考虑基态的简并就可以了,基态简并度。比如:计算三重态的O2的 ,;单重态的CO分子的 ,此时。
(2)平动分子配分函数:
理想气体模型下,平动配分函数为:
其中m为分子质量,相当于单分子占体积,P为气体分压。平动配分函数是唯一和压力有关的配分函数,可见分压P越小,qtrans越大。lnqtrans对温度T做偏导数,可得:
可得,平动对熵的贡献为:
平动对内能的贡献为:
平动的内能和焓的校正和配分函数没有关系,只和温度有关,随温度升高线性增加。平动熵校正和温度与气体压力有关。
(3)振动分子配分函数:
振动对配分函数、熵、内能和热容的贡献由每个振动模式的贡献之和(或乘积)组成,并且只考虑实频,忽略虚频。对于非线性分子来说有3N-6个振动频率,对于线性分子来说有3N-5个振动频率。以势能面最低点(Bottom of the well)为零点计算qvib, 此时谐振近似下的配分函数为:
其中 vi代表各个振动频率,同样把qvib带入到各热力学量的计算公式中,可得内能校正为:
其右边括号中的第一项(1/2)即为零点振动能(ZPE)的贡献,0K时分子振动有零点振动能(ZPE),对应0K下(振动基态)时核振动的能量。值得注意的是零点振动能是在任何情况下都存在,但是DFT计算得到的能量又没有包含这一部分,所以,ZPE是做自由能校正的时候必须要计算的内容。在谐振近似下:
振动熵*Svib*校正为:
可以观察到 -TSvib的第一项正好和Uvib的第二项相互抵消,所以实际计算的过程中只需要计算这一部分就可以了,这一项受频率影响比较敏感。准确计算振动配分函数,特别是低频模式的贡献是准确计算热力学数据最关键也是最困难的地方。频率越低的振动模式对ZPE的贡献越小,但是由于对Svib的贡献越大(因为更容易激发到其振动激发态),因此对升温造成的熵增贡献越大。这是低频振动对熵的贡献,温度越高,振动频率越小,校正的自由能越低。
(4)转动分子配分函数:
对于线性分子:
对于非线性分子:
其中为转动对称数,IA、IB、IC为转动惯量。带入热力学量的公式可得到,对于线性分子:,;对于非线性分子:,
3、实际案例分析
3.1 计算各配分函数贡献
我们实际选择CO为例计算。平动贡献:
298.15 K,101.325 kPa条件下,摩尔质量为14的1 mol CO的平动配分函数为:
则平动内能和平动熵的贡献为:
转动贡献:
CO的转动惯量,在298.15K时的转动配分函数为:
则CO分子的转动内能和转动熵贡献分别为:
振动贡献:
CO分子的伸缩振动大约为2130 cm-1,其振动熵的贡献几乎可以忽略:
同样除去ZPE校正,CO分子的振动内能也几乎可以忽略不计。但是CO对ZPE的贡献则比较明显,为:
这里并不是说所有的分子振动熵和内能贡献都很小,一般来说,只有低频率的振动才有较大的熵贡献,高频振动一般只对ZPE有较大贡献。
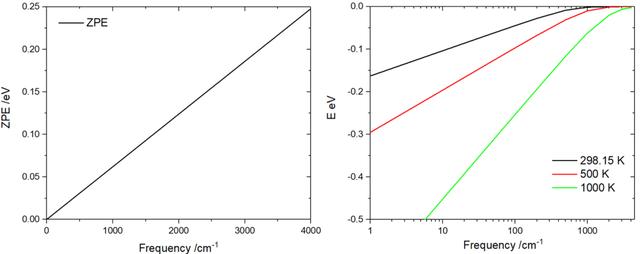
图中可以看出,ZPE的能量和频率成正比,1000 cm-1的频率其ZPE的贡献值约为0.062 eV,50 cm-1的频率其ZPE的贡献值约为0.003 eV。振动熵的贡献则会随着频率的降低迅速增加,在298K下,1000 cm-1的频率其振动熵贡献为-0.001 eV,50 cm-1的频率其振动熵贡献为-0.062 eV。而且随着温度升高,比如在1000K时,50 cm-1的频率其振动熵贡献可以高达-0.313 eV。
补充说明:由于一些吸附分子的受阻平动/转动会产生一些不准确的低频振动,这部分低频振动往往在高温条件下会产生巨大的振动熵校正误差,所以一些文献里吧低于50或60 cm-1的振动贡献都按照50或60 cm-1计算其振动的热力学量贡献。比如:[J. Am. Chem. Soc. 2017, 139, 130−136]。文献中给出的理由是:Note that very low frequency modes were obtained in some cases, because the explicit water molecules are not properly constrained by the hydrogen bonding network present in water bulk. Such low frequency modes can cause unphysically large entropy contributions, so they were reset to a threshold value of 60 cm−1, corresponding to the acoustic translational mode of the six-member rings in water bulk.[J. Chem. Phys. 1967, 46, 1271; J. Phys. Chem. B 2013, 117, 10046]
3.2 计算分子自由能校正
在文献中我们常见的分子自由能校正公式一般写为:
想要得到分子自由能G,首先要知道分子的电子能量,这个能量可以直接由DFT计算得到,然后加上零点振动能ZPE,内能校正,或者直接写成焓校正值,这里所谓的指的是从0K 升温到 TK时能量的变化。有的文献中也写成热容积分的形式 或 ,H最后再加上熵校正的贡献。这就是完整的计算一个孤立分子的自由能校正的方法。在T = 0 K 条件下,只需要做ZPE的计算即可。在温度T > 0 K条件下:
以CO分子为例,通过查询热力学数据库(JANAF-NIST)可得到在标况(298.15K和1bar)下,CO分子的熵为。其平动熵最大,为,转动熵为,其振动熵则可以忽略。其熵贡献能量总共为。对比来看,CO分子在标况下的焓校正值则小的多,仅为。
压力对分子平动的影响比较大,而温度又会同时影响平动、转动、振动的贡献。这些环境因素的变化对分子的热力学量校正影响巨大,会直接导致吸附自由能的剧烈变化。为了更直观的展示温度和压力对分子热力学量的影响,我们以CO分子和乙烯分子为例。计算了零点能、焓、熵、吉布斯自由能校正值随着温度和压力变化曲线。
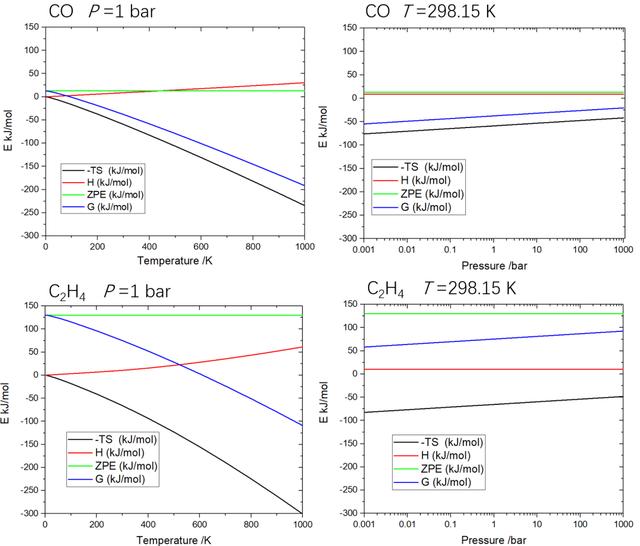
由此可见,随着温度的升高,熵对自由能的贡献增加明显,会使得分子整体自由能量迅速下降。而内能、焓、或热容校正贡献则要小得多,所以在一些文章中也直接忽略这一项,把自由能校正写为如下的形式,对小分子来说这在常温下会带来大约左右的计算误差。
原子数越多的分子其振动模式也越多(3N-6),振动贡献的ZPE校正值也就越大。尤其是含有更多H原子的分子,由于C-H,O-H,N-H,H-H等化学键的振动波数普遍在3000cm-1以上,对ZPE的贡献则比较的明显。而H-H键的振动更是高达4395cm-1,一个氢气分子的ZPE贡献就有0.27eV。所以涉及到氢原子参与得反应,做ZPE的校正非常的重要。比如合成氨反应 反应总ZPE校正贡献为-0.3431eV。(b3lyp/6-311g*优化并计算频率,ccsd(t)/cc-pvtz计算单点能)
表1:使用Gaussian16B程序,b3lyp/6-311g*优化并计算频率,ccsd(t)/cc-pvtz计算单点能,得到的电子能量,在标况下计算的零点能、焓、熵、吉布斯自由能校正值
| 振动频率 (cm-1) | (eV) | ZPE (eV) | (eV) | (eV) | (eV) | (eV) | |
|---|---|---|---|---|---|---|---|
| N2 | 2447 | -2976.1692 | 0.1517 | 0.0899 | -0.5915 | -0.3499 | -2976.5191 |
| H2 | 4394 | -31.9004 | 0.2724 | 0.0899 | -0.4024 | -0.0401 | -31.9405 |
| NH3 | 1123,1751,1751,3465,3587,3587 | -1536.6903 | 0.9461 | 0.1035 | -0.5941 | 0.4555 | -1536.2348 |
表2:使用 VASP 5.4.4程序,500eV截断能,不带后缀赝势,优化并计算频率,得到的电子能量,在标况下计算的零点能、焓、熵、吉布斯自由能校正值
| 振动频率 (cm-1) | (eV) | ZPE (eV) | (eV) | (eV) | (eV) | (eV) | |
|---|---|---|---|---|---|---|---|
| N2 | 2462 | -16.6077 | 0.1526 | 0.0899 | -0.5923 | -0.3498 | -16.9575 |
| H2 | 4271 | -6.7702 | 0.2648 | 0.2648 | -0.4031 | -0.0483 | -6.8185 |
| NH3 | 989,1611,1612,3419,3544,3547 | -19.5387 | 0.9128 | 0.1040 | -0.5954 | 0.4214 | -19.1173 |
3.3 误差在哪
最后,我们会看到 反应计算总包反应的自由能变的误差非常的大,甚至有定性的错误,这些误差来源主要有两部分,一是振动频率,二是电子能量计算误差。
(1)振动频率
振动频率的误差来自两方面,一是计算频率的时候采用谐振近似,二是计算级别本身有误差。所以直接通过计算得到的振动频率和实际频率有一定偏差,在量子化学计算中人们往往会给计算得到振动频率添加频率校正因子,校正不同热力学量时的校正因子也不尽相同,详细的校正参数可以在文献(JPC100 16502)中查到。使用VASP程序等第一性原理计算程序,用PBE泛函结合平面波基组计算的频率误差并没有文章作过系统性的误差评估,所以在大部分文章中还是直接使用计算得到的频率。
振动频率也会影响两方面,一是ZPE,二是振动熵。低频振动(<50 cm-1)往往十几个波数的计算误差就会引起大于0.1 eV的熵校正误差。高频振动对ZPE的贡献较大,对于一个3200cm-1的振动,5%的频率计算误差就会带来大约0.01eV的误差,而且含有N个原子的分子有3N-6个振动自由度,ZPE的误差累加起来就很可观了。
(2)电子能量
受限于计算方法的精度,泛函误差,赝势、基组不完备等问题。直接DFT计算出来能量往往会有~0.1 eV左右的误差,尤其对于双原子小分子误差更甚。VASP手册上明确说明,基于平面波基组的程序在处理双原子分子的时候,比如CO、O2、N2、F2、P2、S2、Cl2、等分子,计算出来的电子能量不准确,想要得到靠谱的结构需要使用"_h"更硬的赝势,并配合更高的平面波截断能。在表2计算得出合成氨反应的总自由能变化为-0.82 eV,而在热力学表上查到的数值是-0.34 eV。
(3)解决办法
在Gaussian等程序为主的量子化学计算中,往往是通过引入频率校正因子消除误差。在使用第一性原理的表面催化反应计算中,则常采用通过实验热力学数据反推的方法,为了满足总包反应和热力学表一致,往往不直接计算其中双原子小分子的能量,而是用热力学数据反推。例如: 的总自由能变是-0.34 eV,NH3的计算得到的自由能是-19.12 eV,H2的计算得到的自由能是-6.82 eV,那么N2的自由能直接用以上数据反推出来时-17.44 eV。后续在计算N2参与的反应时,比如吸附、脱附过程,都直接用-17.44 而不是 -16.96。这样的操作处理在表面催化反应中极为常见。类似的还有:的反应自由能能量为-4.92 eV,其中 O2的能量需要反推的到;的反应自由能能量为-0.21 eV,其中CO或者O2的能量需要反推得到。
4、VASPKIT做自由能校正操作
4.1 气体分子自由能校正
计算频率校正需要首先计算频率,这里以氧气分子在Au(111)表面的吸附为例,计算吸附自由能:
我们先看怎么算,再看和怎么处理。VASPKIT已经把计算热力学量的各种校正公式都编程好了,用的时候只需要气体分子的 1、所有振动频率, 2、气体分压, 3、环境温度, 4、分子的基态电子多重度。这四项就可以了。频率计算在上一节中我们已经详细讲述了。其余3项在vaspkit的502功能中依次输入。氧气分子频率计算完成之后运行grep cm OUTCAR,查看所有频率:
grep cm OUTCAR 1 f = 46.979964 THz 295.183821 2PiTHz 1567.082879 cm-1 194.293584 meV2 f = 1.952595 THz 12.268518 2PiTHz 65.131565 cm-1 8.075288 meV3 f = 1.120777 THz 7.042052 2PiTHz 37.385108 cm-1 4.635164 meV4 f/i= 0.006984 THz 0.043884 2PiTHz 0.232971 cm-1 0.028885 meV5 f/i= 1.046106 THz 6.572876 2PiTHz 34.894327 cm-1 4.326347 meV6 f/i= 1.294104 THz 8.131095 2PiTHz 43.166663 cm-1 5.351986 meV
看到三个虚频,这对气态分子非常正常,因为分子振动自由度是3n-6,线型分子是3n-5。所以氧气分子只有1个振动自由度,其余的5个小频率都属于平动和转动自由度在振动上的投影,计算的时候直接无视。运行VASPKIT,使用主功能5,子功能502,输出如下:
------------>>502 -------------------------- Warm Tips -------------------------- See An Example in vaspkit/examples/thermo_correction/ethanol.This Feature Was Contributed by Nan XU, Jincheng Liu and Sobereva.Included Vibrations, Translation, Rotation & Electron contributions.GAS molecules should not be with any fix.-->> (01) Reading Structural Parameters from POSCAR File...-->> (02) Analyzing Molecular Symmetry Information...Molecular Symmetry is: D(inf)hLinear molecule found! --------------------------------------------------------------- Please input Temperature (K)!298Please input Pressure (Atm)!1Please input Spin multiplicity!--(Number of Unpaired electron 1)3------------>>-->> (03) Extracting frequencies from OUTCAR...-->> (04) Reading OUTCAR File...-->> (05) Calculating Thermal Corrections...U(T) = ZPE Delta_U(0->T)H(T) = U(T) PV = ZPE Delta_U(0->T) PVG(T) = H(T) - TS = ZPE Delta_U(0->T) PV - TSZero-point energy E_ZPE : 2.240 kcal/mol 0.097144 eVThermal correction to U(T): 3.723 kcal/mol 0.161442 eVThermal correction to H(T): 4.315 kcal/mol 0.187121 eVThermal correction to G(T): -10.309 kcal/mol -0.447028 eVEntropy S : 205.328 J/(mol*K) 0.002128 eV/K
这里输出的关键信息是:
用O2分子的电子能量,加上其自由能校正值(-0.447 eV),就得到O2分子的自由能。注意这里的O2分子的电子能量,不能读VASP计算频率的最后一步的能量,因为它不是处于势能面极小值的,而是有限位移方法产生的偏离极小值的一个点。要读取到此处极小值点的能量还要去看结构优化最后一步的能量(-9.863 eV),这才是势能面极小值的能量。
注:文献中有的校正方法没有考虑热容部分的校正,是因为这些文献的作者认为U(T)的贡献很小可以忽略,实际上,对于氧气分子这部分贡献有大约有0.0643 eV,可见对于精度要求稍高的计算,忽略热容校正都是不合理的做法。
4.2 液体分子自由能校正
一些化学反应往往涉及到液相体系,比如电催化计算。所以算准溶液分子的能量也非常关键。第一性原理计算对于校正溶剂化计算比较困难,目前已有的隐式溶剂模型有vaspsol 的 GLSSA13 Linear PCM、JDFTx的CANDLE、QE和CP2K的SCCS等。实际上我们要想得到一个液相体系的自由能,并不需要直接计算溶剂化的分子,而是可以利用一些已知的实验数据,配合计算得到我们想要的自由能,这样比直接计算液相分子要准确的多。下面分享几个方法:
(1)利用饱和蒸汽压下的气态和液态的化学势相等关系,通过计算气态分子在饱和蒸汽压下的自由能,即得到液体的自由能。这仅限于可以查得饱和蒸汽压的分子,比如我们常用得水分子,在常温下得饱和蒸汽压约为0.035 bar。在VASPKIT里计算分子自由能时候输入相应得压力0.035 bar就可以了。应用案例:ORR,OER电催化反应计算中H2O(l)的能量。
(2)如果想要计算水溶液中某离子的自由能,比如1mol/L Pt2 的自由能,直接计算离子的溶剂化能太困难了,可以利用的是标况下的标准电极电势U0。2 的自由能就带入下式得到。
(3)用隐式溶剂化模型计算溶解自由能,用vaspsol等隐式溶剂计算的单点能减去同结构没有隐式溶剂的能量即可得到溶解自由能。溶质在溶剂环境标况下的自由能为:
其中,是气相标况下该分子的能量,是溶解自由能,是把1 atm 气态的溶质分子挪入到溶剂中成为1 mol/L 溶剂中其浓度改变造成的自由能变。这部分在电化学一章中详细讲解。
4.3 吸附分子自由能校正
不同于气态分子的热力学校正,表面吸附分子和载体形成化学键,从而限制吸附分子的平动和转动自由度,所以平动和转动对于熵和焓的贡献都会显著降低(Hindered translator / hindered rotor model),但是这并不意味着他们没有贡献。一般大家都接受的方法(文献里最常用的方法)就是把这一部分贡献归到振动里,也就是说表面吸附分子的 3N 个振动(虚频除外)都用于计算热力学量的校正计算,而忽略表面受阻平动和受阻转动的实际的贡献。想要精确计算表面分子受阻的平动和转动贡献,可以用ASE程序的模块算,ase.thermochemistry.HinderedThermo。
还是以氧气分子吸附在Au(111)表面为例,为了计算吸附过程的吸附自由能,
吸附模型可以用只有一个氧原子的O/Au(111)模型,虽然计算模型里只有一个氧原子,但是对于周期性模型来说有无数个氧原子,这里用一个氧原子和两个氧原子吸附的模型仅仅是覆盖度不一样。对于载体2*2的Au(111)模型,覆盖度是1/4ML。

grep cm OUTCAR查看频率结果,得到三个实频,都是O原子振动产生的。
1 f = 10.904836 THz 68.517103 2PiTHz 363.746154 cm-1 45.098792 meV2 f = 10.827330 THz 68.030119 2PiTHz 361.160834 cm-1 44.778253 meV3 f = 10.751668 THz 67.554721 2PiTHz 358.637024 cm-1 44.465340 meV
如果计算的是O迁移的过渡态频率,得到两个实频和一个虚频。计算自由能的时候不包括虚频。
1 f = 12.609563 THz 79.228223 2PiTHz 420.609746 cm-1 52.148981 meV2 f = 12.052440 THz 75.727713 2PiTHz 402.026105 cm-1 49.844902 meV3 f/i= 3.964289 THz 24.908363 2PiTHz 132.234445 cm-1 16.394988 meV
最后运行VASPKIT,使用功能501
------------>>501 -------------------------- Warm Tips -------------------------- This Feature Was Contributed by Nan XU, Qiang LI and Jincheng LIU.See An Example in vaspkit/examples/thermo_correction/ORR.Only vibrations! No Translation & Rotation & Electron contributions. --------------------------------------------------------------- Please Enter The Temperature (K):------------>>298-->> (01) Reading OUTCAR File... -------------------------- Summary ---------------------------- Neglect PV contribution to translation for adsorbed molecules.To avoid abnormal entropy contribution,frequencies less than 50 cm-1 are set to 50 cm-1.U(T) = H(T) = ZPE Delat_U(0->T)G(T) = H(T) - TS = ZPE Delat_U(0->T) - TSTemperature (K): 298.0Zero-point energy E_ZPE : 1.549 kcal/mol 0.067171 eVThermal correction to U(T): 2.205 kcal/mol 0.095639 eVThermal correction to H(T): 2.205 kcal/mol 0.095639 eVThermal correction to G(T): 1.208 kcal/mol 0.052364 eVEntropy S : 14.011 J/(mol*K) 0.000145 eV
只需要输入温度即可,得到的G(T)就是吸附分子的自由能校正值0.052 eV,因为吸附分子不能在空间中自由移动了,所以PV项贡献认为是0,得到U和H的校正值相等,加上O/Au(111)优化的最后一个结构的能量就得到体系的自由能。
| (eV) | (eV) | (eV) 298 K | |
|---|---|---|---|
| Au(111) | -61.696 | 0 | -61.696 |
| O2 | -9.863 | -0.447 | -10.310 |
| O/Au(111) | -66.751 | 0.052 | -66.699 |
可得
4.4 固体自由能校正
固体自由能校正需要用计算声子色散关系,结合phonopy计算比较方便。phonopy我们在频率计算一章中已经详细讲解了,算完声子色散关系之后,准备mesh.conf文件:
ATOM_NAME = AuDIM = 2 2 2MP = 15 15 15FORCE_CONSTANTS = READTMAX = 2000TSTEP = 100
运行phonopy -c POSCAR-unitcell mesh.conf -t
phonopy -c POSCAR-unitcell mesh.conf -t__ __ | |__ ___ _ __ ___ _ __ _ _| '_ \| '_ \ / _ \| '_ \ / _ \ | '_ \| | | || |_) | | | | (_) | | | | (_) || |_) | |_| || .__/|_| |_|\___/|_| |_|\___(_) .__/ \__, ||_| |_| |___/2.7.0Python version 3.6.8Spglib version 1.15.1Phonopy configuration was read from "mesh.conf".Crystal structure was read from "POSCAR-unitcell".Unit of length: angstromMesh sampling modeSettings:Sampling mesh: [15 15 15]Supercell: [2 2 2]Spacegroup: Fm-3m (225)Use -v option to watch primitive cell, unit cell, and supercell structures.Force constants are read from "FORCE_CONSTANTS".Mesh numbers: [15 15 15]Number of irreducible q-points on sampling mesh: 120/3375Calculating phonons on sampling mesh...Calculating thermal properties...# T [K] F [kJ/mol] S [J/K/mol] C_v [J/K/mol] E [kJ/mol]0.000 7.1127368 0.0000000 0.0000000 7.1127368100.000 4.1502910 75.3026229 84.0490530 11.6805533200.000 -6.8271160 138.2919034 95.4675013 20.8312647300.000 -22.7430976 177.5391120 97.8221504 30.5186360400.000 -41.9764138 205.8134933 98.6659543 40.3489835500.000 -63.7012219 227.8773533 99.0600543 50.2374548600.000 -87.4201669 245.9589171 99.2750812 60.1551834700.000 -112.8012488 261.2727674 99.4050598 70.0896884800.000 -139.6071837 274.5523542 99.4895517 80.0346997900.000 -167.6599513 286.2740841 99.5475388 89.98672441000.000 -196.8210646 296.7647272 99.5890464 99.94366271100.000 -226.9797199 306.2580878 99.6197733 109.90417671200.000 -258.0452519 314.9271881 99.6431527 119.86737381300.000 -289.9421013 322.9036436 99.6613529 129.83263541400.000 -322.6063303 330.2898928 99.6757976 139.79951971500.000 -355.9831331 337.1672236 99.6874530 149.76770231600.000 -390.0250102 343.6012189 99.6969936 159.73694001700.000 -424.6903984 349.6455559 99.7049016 169.70704671800.000 -459.9426237 355.3447230 99.7115293 179.67787771900.000 -495.7490864 360.7360027 99.7171387 189.64931872000.000 -532.0806182 365.8509482 99.7219284 199.6212782Summary of calculation was written in "phonopy.yaml".____ _ __ __| |/ _ \ '_ \ / _` || __/ | | | (_| |\___|_| |_|\__,_|
phonopy自动输出不同温度下的自由能F,熵S,热容Cv,内能E。
5 查JANAF-NIST表计算气体分子的自由能校正
通过实验热力学的数据库,比如JANAF-NIST表也可以来估算氧气分子的自由能校正值,但是热力学数据表是没法直接给出ZPE校正量的,需要计算频率或者根据实验测的频率值计算。JANAF-NIST是美国国家标准与技术研究院提供的数据:https://janaf.nist.gov/ 可以查到常见分子,在标准压力0.1 MPa 和不同温度下的热力学校正量。其中的S°是熵,H-H°(Tr)是在不同温度下的焓和298.15K时的差值,由于第一性原理计算都是0 K下的能量,所以校正的时候还是要参考0K的焓去校正。
Oxygen (O2) O2(ref)Enthalpy Reference Temperature = Tr = 298.15 K Standard State Pressure = p° = 0.1 MPaJ·K-1 mol-1 kJ·mol-1T/K Cp° S° -[G°-H°(Tr)]/T H-H°(Tr) fH° fG° log Kf0 0. 0. INFINITE -8.683 0. 0. 0.100 29.106 173.307 231.094 -5.779 0. 0. 0.200 29.126 193.485 207.823 -2.868 0. 0. 0.250 29.201 199.990 205.630 -1.410 0. 0. 0.298.15 29.376 205.147 205.147 0. 0. 0. 0.300 29.385 205.329 205.148 0.054 0. 0. 0.350 29.694 209.880 205.506 1.531 0. 0. 0.400 30.106 213.871 206.308 3.025 0. 0. 0.450 30.584 217.445 207.350 4.543 0. 0. 0.500 31.091 220.693 208.524 6.084 0. 0. 0.600 32.090 226.451 211.044 9.244 0. 0. 0.700 32.981 231.466 213.611 12.499 0. 0. 0.800 33.733 235.921 216.126 15.835 0. 0. 0.900 34.355 239.931 218.552 19.241 0. 0. 0.
以氧气分子为例,是VASP计算得到的电子能量,是计算频率之后得到的,表中298.15 K下的:
由此可见,用vasp VASPKIT得到的自由能和查找热力学表的实验值几乎完全一样,说明在高精度计算条件下,使用VASPKIT可以很好的校正气体分子的自由能的。但是对于一些复杂的分子来说,校正误差和实验值可能稍大。
,