没有为什么,就是一闪而过的念头记录了下来。
限于水准,所以搞不出花里胡哨。
好在高考追求稳定,大多套路都有迹可循。这些题,有的来自原创,有的来自改编,有的来自拼凑,有的来自重组,不一而足。
押中了,也就中了;没押中,权当玩笑。
反正无伤大雅,明天还是明天,我还是我。
捧场随意,当切莫当真。
有些事,看似言之凿凿,却未必不是捕风捉影。
以上,有的是对自己说的,有的是对你说的。
江湖险恶,不行就撤。


高考不是竞赛,基础仍占半壁。
对任何人来说,无视基础都是大忌。瞅着白花花的分数从指尖划过,犹如切肤之痛。基础不失分是追求的终极目标,我们是绝对不会作壁上观的。
三角函数,考点甚多,公式繁琐。
本题考查三角恒等变换,融入诱导公式、同角基本关系式以及二倍角公式。简单到爆,尤其适合放在第4、5题的位置,直接送分,毫不吝啬。
2 套路:手足无措,抑或从容不迫

1.命题背景:
三角函数的性质与解三角形,才是本章的核心,而三角函数的概念、诱导公式、三角恒等变换只能算边角料,往往作为其中的步骤,惊鸿一瞥。
即便是这无足轻重的考点,其中包含的内容也非同小可。
(1)三角函数的定义:

定义是最基本的概念,也是基本属性的界定与规范。
三角函数的定义可以借助单位圆,也可借助三角函数线(三角函数的几何表示),其符号可简记为“全正切余”。
有了定义,公式性质便顺理成章。
(2)同角基本关系式:

这些公式都可用定义推导,但记住更好,包括几个不常见但很好用的。倘若非要追本溯源,人教B版新教材,对正割、余割、余切等三角函数均有介绍。
(3)诱导公式:

诱导公式是将大角三角函数转换为小角三角函数的工具,是一般与特殊的纽带。诱导公式可简记为“奇变偶不变,符号看象限”。
(4)两角和与差的三角函数:
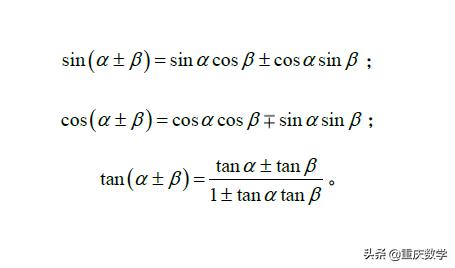

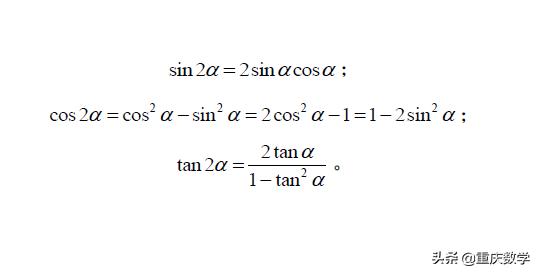
无论是诱导公式,和差公式,还是二倍角公式,目的都是为了简化运算。
(6)万能公式:

这是相对陌生的公式,既然叫“万能”,想必一定有内涵。先了解,未来还有机会遇上,它对双曲函数也有着类似的作用(后续介绍)。
平素做题无算,千算万算,还是命题划算。命题其实根本没那么麻烦,一闪而过的念头就够了。但如果是那样,会显得味同嚼蜡,苍白无力。
2.命题手法:
基石已铺就,接下来就是随意组装。
命制一道选择题,一道基础题送分题,所以内容不宜太多,计算不宜繁琐。两三个知识点最好,短小精悍,言简意赅。

当然,这是我惯用的伎俩,不代表什么,无非是从特殊到一般。
3.命题目标:
借助三角恒等变换考查代数运算,由此窥伺熟练程度和变形技巧。

有了法1与法2,超纲也就无稽之谈。而法3与法4用到了二级结论,更快更爽。套路大相径庭,本质殊途同归。
4 操作:形同陌路,抑或一见如故







