摘 要: 介绍了利用扇形激光截面扫描方式对物体进行轮廓扫描与体积计算的原理与方案。同时阐述了其中体积计算的核心思路与实现方式,重点指出了对物体进行点云数据采集的几种方式,包括构建虚拟模型的构架与思路。在实现中,着重介绍所采用的灰度距边缘检测算法,用以识别被测物体与背景之间的边缘结构,此外还提出了双面体积拼接算法,通过双面测量、拟合成为整体的方式,实现了物体的双面拼接测量,使得该方案具有更加广泛的适用性。最后,通过数次实验结果的误差分析与重建三维模型和实物的观察对比证实了本方案能够确切、可靠地完成物体的三维体积扫描。
0 引言
在物流行业中,对于运输货物体积的控制,往往有着明确的要求和标准。例如在航空运输中,准确获知货物的重量和体积,对于飞机的配重有很重要的作用。体积目前大多是靠人工目估,精确性比较差,因此,需要使用规范化、自动化的室内货物体积测量方案来提高测量精度[1-3]。
本文将着重介绍使用扇形激光截面扫描技术对中小型货物进行快速体积扫描,以截面扫描的方式获取目标单个截面的测距数据,横向采集的同时对目标进行纵向间隔采样,获取类似二维矩阵的点云数据,整合之后即可获取目标整体的高度点云信息,以用于后续的体积计算与三维建模。本方案的优点主要体现在实现快速、精确度高并且误差可控等几方面。对于中小型目标进行体积测量时需要着重考虑由于激光直线传播所带来的遮挡问题,针对于此,利用sobel算子[4-6]进行两次单面边缘检测的方式给出了解决方案。
1 设备选型
文中所提及的测量设备选取SICK激光扫描测距仪,扫描范围:-135°~ 135°可调;扫描角分辨率:0.25°/0.5°可调;系统误差:10 mm/typ.±30 mm;工作范围(最大值10%反射率):20 m;扫描频率:25/50 Hz可调。

扫描方式为如图1所示的扇形区域扫描。
2 三维测量原理及数学模型
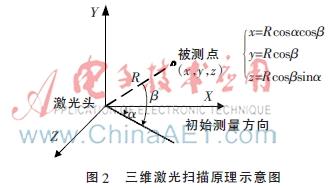
激光测距仪主要采用激光测距技术,同时根据测量点所在空间的三维坐标与偏转角三角函数关系获得后期计算、构建三维模型中所需要的各种信息。激光测距仪采取飞行时间算法,扫描仪记录并处理激光发射与返回之间经历的时间,即可获得所测距离R,同时由于物体与激光头位于三维坐标之内,存在原点与偏移角的问题,因此需要获取激光头每次测距时与初始0角度之间的水平方向的夹角α与垂直方向的夹角β,三者结合计算即可获得被测点的三维坐标[7-8]。如图2所示。
通过以上原理进行体积计算时,采取离散量化,体积累加的方式。首先,根据离散的测量点对三维物体进行柱体分隔;然后计算每个小柱体的体积;最终累加所有体积,获得待测物体的整体体积。
获得待测物轮廓高度信息时主要提取每个待测点在Y(初始垂直)方向上的距离信息,将激光头到地面的距离H0与激光头与物体在X方向上的投影距离Hy作差,结果即为物体表面轮廓的高度H[9]。离散体积计算示意图如图3。

对于待测物体的总体积用V表示,数学关系可表示为:
根据角度关系可知,式(1)中?驻Si不为定值,?驻Si=?驻xi?驻xi且与偏转角度α有关;柱体高度Hi=H0-Hy。

在本次测量方案中,选择扇形截面激光测距仪,该扫描仪以类似于图4的方式在垂直截面上对物体进行列扫描,扇形扫描范围最大270°(±135°)。以角分辨率0.5进行间隔角度采样,扫描范围内共可获取540个离散点的测距信息。单次扇形扫描完成后数据通过网络接口成组发送。

单次截面扫描情况(Y-Z轴方向)如图5所示,截面扫描仪对截面上方轮廓进行激光测距采样,扫描仪返回激光头到各采样点的距离Li以及与中心线的夹角值。由三角函数关系可以获得采样点的三维坐标Mi(zi,yi),其中以M1点为例:
y1=L-L1cosα(2)
z1=L1sinα(3)
由式(2)、式(3)可得出,M1与M2之间的距离为:
|M1-M2|=|L1sinα-L2sinβ|(4)
同理,获得其余采样点的信息[10-11]。
对物体进行整体扫描之后,以每个采样点为中心进行如图3所示的体积分割,由于已知每个模拟小柱体的高Hi为:
而宽度
x可以由扫描仪前进的速度v与列采样间隔t决定:
由式(1)可求每个分割小柱体的体积,由此可推得被测物体体积的整体表达式如下:
3 系统构架
三维激光体积测量系统中,首先由激光扫描仪与运动轨道系统负责收集待测物体的表面轮廓信息,软件即对数据进行处理,转化为二维点云高度信息阵列进行保存,再根据图3所示的体积分割算法对待测物体体积进行整体测量,并将结果输出显示器或保存[12]。
三维激光体积测量系统的实现流程图如图6所示。
4 数据采集过程与改进
扇形截面扫描仪在单一方向上匀速进行列扫描,获取整个物体单侧表面的点云高度信息。但当物体单侧表面对背侧表面形成遮挡时,仅获取单侧表面的数据无法准确地计算出被测物体实际体积,因此设计了改进型的双面拼接测量方式,如图7所示。

在双面拼接采集的情况下,摄像头将从P1、P2左右两个位置对被测物体分别进行数据采集,由于每次采集时,背面的情况摄像头无法获取,因此每次采集只计算当前可见部分的二维高度点云数据,通过边缘检测获取临界面S的高度信息。将物体可视表面与临界面的二维高度点云数据进行作差处理,再进行体积计算,即可获得两部分分别的体积信息,两者叠加即为待测物体最终体积。
5 sobel算子边缘检测
在使用双面拼接采集方式时,激光头到临界面的距离随测量实际情况而确定,需要使用边缘检测技术来确定临界面的位置。由于所采集、整理后的点云数据以二维矩阵的形式存储,边缘点存在数值上的跳跃,与灰度图像边缘分析模型类似,可以使用sobel算子进行边缘检测,A代表二维点云数据信息,式(9)、(10)中使用Gx、Gy分别完成横向与纵向上的边缘检测。

点云数据中可以用式(11)结合每点的横向、纵向梯度值获得梯度大小G,当梯度值G大于阈值?赘时,可以判定此处为边缘,即所求临界面边缘位置。
理想的灰度边缘模型按照阶跃边缘模型分布,而实际中的边缘灰度模型与阶跃模型有所差异,因此,使用sobel算子检测的边缘不够尖锐,因此需要理想的阶跃边缘模型划分出准确边缘的位置。一阶边缘模型被认为是由所获取的被测物体表面轮廓高度信息与位置信息在二维坐标系中分布的离散点所组成的[13-14]。理想的边缘由三个离散点组合而成:边缘位置Pi、与边缘相邻的两个点Pi-1、Pi 1。如图8所示,实线表示理想模型,离散点表示实际边缘点。

若Pi点为边界值,那么应满足公式(12)中的条件,其中?字为边缘点与前一点的差值阈值,δ为边缘点与后一点的差值阈值。
使用sobel算子与阶跃阈值结合分析的方法,可以确定出图7中双面测量时的临界面S,进而获得S面边缘位置的距离信息。
6 三维模型重建及计算结果
6.1 单次扫描方案结果论证
使用单次扫描方式,获得堆体货物的高度点云信息,将数据以EXCEL格式进行保存,再导入MATLAB中进行三维显示,可获得被测物体的三维重建模型。实验中所使用的堆体重建后如图9所示。

被测堆体由4部分组成,实际测量体积分别为0.264 m3,0.060 m3,0.052 m3,0.029 m3。总体积0.405 m3,实际测量体积与误差对比如表1所示。

由表1可见,多次测量误差均控制在5%之内。
对于实验测量方案做了大量的实际测量工作,对不同光照条件、不同材质物体以及不同采集速率下的实验结果做了误差比对,结果证明,此方案能够在大多数情况下完成准确的体积测量任务,结果稳定、可靠。
6.2 双面拼接扫描方案结果论证

使用双面拼接扫描方法对如图10所示的菱形柱体对象进行双面拼接扫描测试。由于纵向上无法提取有效的临界面边缘信息,因此仅使用横向sobel算子实现边缘检测,选取阈值Gy≥700。最终三次测量取平均值获得的实验结果为:左侧体积0.149 m3,右侧体积0.123 m3,实际测量结果总和0.272 m3,物体实际体积0.264 m3,误差 0.008 m3,误差率3.03%。实验结果正确,误差在可接受范围内。
7 结论及误差分析
本文采用扇形界面扫描的方式以及改进型双面拼接扫描算法提高了方案的准确度与适用性。通过三维模型重建,有效地提高了测量结果的可视性,方便直观地验证了扫描数据的正确与否。大量的实际测量实验表明,两种测量模式的测试结果误差普遍小于0.02 m3,误差可控。
系统误差方面,由体积计算原理式(1)可知,误差主要由分隔小柱体体积与原本曲面之间存在的量化误差形成,因此尽可能小地分割柱体,减小式(8)中的角度分辨率?琢i与激光扫描仪前进的速度v,可以提高计算结果的准确度。而从测量误差方面来看,经过多次实际测量确定本方案中的激光扫描仪测距误差在0.02 m左右。同时,由于激光扫描仪的内部结构特点,光照、温度与物体表面材质的变化都会对激光测距的结果产生微弱的影响。
需要说明的是,本文所提及方案的实施需要配套的机械架构、协调传动设备,因此在实际试验测量中核心思想不变,微调了部分测量方式,但不影响实验结果的准确性与可靠性。
参考文献
[1] Chen Junmei, Liu Xiong, Zhao Zuoxi, et al. Research on landscape environment with 3D-reconstruction and volume measurement of fruit tree canopy based on Kinect[J]. Advanced Materials Research, 2013,788:480-485.
[2] ROBERT S, MACJ K, WOJCIECH Z, et al. Automated full-3D shape measurement of cultural heritage objects[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2009,7391,DOI:10.1117/12.828004.
[3] Pan Bing, Wang Bo, Wu Dafang, et al. An efficient and accurate 3D displacements tracking strategy for digital volume correlation[J]. Optics and Lasers in Engineering, 2014, 58:126-135.
[4] Zhang Jinyu, Yan Chen, Huang Xianxiang. Edge detection of images based on improved sobel operator and genetic algorithms[C]. Proceedings of 2009 International Conference on Image Analysis and Signal Processing, IASP, 2009:32-35.
[5] Gao Wenshuo, Yang Lei, Zhang Xiangguang, et al. An improved Sobel edge detection[C]. Proceedings-2010 3rd IEEE International Conference on Computer Science and Information Technology, 2010:67-71.
[6] 姜志华.基于激光扫描的堆料体积测量系统研究与设计[D].武汉:华中科技大学,2011.
[7] 朱铁军.激光扫描技术测量粮堆体积试验[J].粮食科技与经济,2012,37(4):30-31.
[8] 毕银丽.基于点云数据的株冠体积测量方法[J].科技导报,2013,31(27):31-36.
[9] 吉华,戴健伟,孔令钊,等.基于激光测距的车载沙石体积测量系统[J].仪表技术与传感器,2013(2):42-45.
[10] 韦山.便携式计算机的车载激光扫描盘煤系统研究[D].合肥:安徽农业大学,2004.
[11] 申恒洋.激光盘煤仪的研制[D].南昌:南昌航空大学,2013.
[12] 李长安.基于三维激光扫描的煤堆建模系统设计与实现[J].硅谷,2012(15):53-56.
[13] 邢冀川.利用激光三角法测量货车车厢体积[J].红外与激光工程,2012,41(11):3083-3087.
[14] 张小青.基于四面体的不规则表面文物体积计算[J].测绘通报,2011(10):50-52.
,




