作者 | 刘钝(中国科学院自然科学史研究所)、苏淳(中国科学技术大学数学系)
来源 | 自然辩证法通讯,1984(06):62-74. 原标题《彼得堡数学学派的奠基人——纪念Π.Л.切比雪夫逝世九十周年》.
让所有的人都得到智慧和地位,真正是俄罗斯的而不是外国的。
——Л.Φ.马格尼茨基
在彼得大帝宏伟的改革蓝图中,有一项仿效西方建立科学院的计划,然而由于种种原因,这个柏林科学院的翻版直到彼得大帝去世的1725年才正式建立起来。早期的院士中不乏伟大的数学家,如贝努里兄弟(N.Bernoulli,1695—1726,D. Bernoulli,1700-1782)、哥德巴赫(C.Goldbach,1690-1764)和欧拉(L.Euler,1707—1783)等人,但是他们都是外国人。当时俄罗斯的数学土壤是贫瘠的:没有土生土长的数学家、没有能够引起世界注意的成果、没有大学,甚至没有初等数学教科书。

十九世纪俄国数学家巴夫卢提·里沃维奇·切比雪夫
马格尼茨基(Л.Φ.MarRxuxx,1669—1739)是当时致力于数学教育的学者,本文的题辞就是他写在著名的《算术》一书扉页上的诗句,它清楚地表达了当时一部分先进的知识分子渴望祖国摆脱愚昧落后状态的强烈心情和建设俄罗斯新科学的决心。正是基于这样一种信念,大约一百多年以后,一批优秀的数学家聚集在圣彼得堡,以具有开拓意义的工作和鲜明的风格使这座城市光芒四射,以至德、法、英这些传统数学大国的学者们也不得不刮目相看。领导着这一数学王国、使俄罗斯数学从极端落后境地走向世界前列的就是十九世纪俄国数学家巴夫卢提·里沃维奇·切比雪夫(Mapuyrna Ibsosrq He6uwes,1821-1894)。
迷恋机械和素数的少年
1821年5月16日,切比雪夫诞生于俄国中部卡卢加省的一个贵族庄园。他的父亲列夫·巴甫洛维奇是一个退役军官,曾参加过1812年抵抗拿破仑入侵的战争;母亲阿格拉芙娜·伊万诺夫娜·波茨尼维柯娃出身名门,是个不苟言笑的女人。这对夫妇一共生了五男四女,Π.Л.切比雪夫排行第二。家族纪念馆里,陈列着祖辈们的勋章、绶带和战刀,在这种环境中长大的男孩子们,无疑会把效命沙场视为人间的殊荣。的确,Π.Л.切比雪夫的三个弟弟后来都投笔从戎,其中一个还成了著名的炮兵将军。
有幸的是,我们的主人公没有成为军人而成了学者,幸运是孕育在不幸中的。从童年时起,他的左脚就残疾了,走起路来一跛一拐的。这使父母很失望,也给他幼小的心灵带来了创伤。当孩子们在庄园里玩着攻占堡垒的游戏时,他却只能独坐家中,拿细劈柴、胶木板充当积木来玩。再大一些的时候,他迷上了各种机械,整日钻进磨坊,观看那嘎嘎作响的水车和磨盘的运动;要么就躲进黑暗的储藏室,摆弄那些生锈的锁、废弃的捕兽器和古老的挂钟。这种在孤寂中探索未知世界的童年生活,在很大程度上决定了他日后的道路。
苏哈列瓦娅表姐是一个娴静、端庄而又富有同情心的姑娘,她教切比雪夫法文、音乐和算术。晚年的切比雪夫经常回忆起当年的情景,对这位启蒙老师怀着极深的感情,他一直把表姐的相片珍藏在身边。
切比雪夫十一岁那年,父母带领全家迁居莫斯科。
1828年政府颁布的学校规章恢复了严格的等级制度;一般中学以神学、希腊和拉丁文为主要科目,而象皇村、里含列夫那样的贵族寄宿学校,则是纨绔子弟们庸集的场所,因而雇佣一个好的家庭教师是上流社会里最稳妥的教育子女的办法。
切比雪夫的双亲为孩子们请到了一位出色的家庭教师。波戈列利斯基不但聪明容智、广见博闻,而且还是几本颇为流行的初等数学教科书的作者。他最喜欢这一家里那个腿有些跛的男孩子,建议他去读古希腊学者欧几里得(Euclid,330-275?B.C.)的《原本》。这部古代数学名著一下子攫住了少年切比雪夫的心,那宏伟的逻辑结构、严密的演绎推理以及令人眼花缭乱的定理和图形深深地吸引了他。然而最使他神往的还是书中关于数论的那三章了,因为波戈列利斯基先生告诉他,当代最伟大的数学家高斯(C.F.Gauss,1777-1855)讲过;“数学是科学的女皇,而数论是数学的女皇。”
当他读到第九章第二十个命题时,不禁从心底发出对数学力量的赞美。“没有最大的素数”,这意味着只能被自身和1整除的自然数有无穷多,他钦佩欧几里得深刻的洞察力和灵巧的证明方法,深感素数的分布奥妙无穷。
这种来自心灵深处的震颤对他的一生产生了巨大的影响。1837年,十六岁的切比雪夫怀着虔诚与崇敬的心情踏进了一座科学殿堂,成为莫斯科大学哲学系物理数学专业的学生。
从经典分析到概率论
莫斯科大学是俄国最古老的一所高等学府,由罗蒙诺索夫(M.B.JIoxorocoB,1711一1765)于1755年所创造,当初仅设哲学、法律、医学三个系,物理与数学时而附属于哲学系,时而独立门户。
年轻的切比雪夫在杰出的数学教育家勃拉什曼(H.A.bpamxar,1796-1866)的指导下开始了正规的数学训练。勃拉什曼生于捷克斯洛伐克的摩拉维亚,1834年起到莫斯科大学任教授,1855年成为彼得堡科学院的通讯院士。他的主要贡献在水利学和最小作用原理方面,数学上特别擅长连分数的理论和计算。切比雪夫后来写过一封信,把自己利用连分数把函数展开成级数的工作归于勃拉什曼在课堂上和私人谈话中给予的启示。该信于1865年9月30日在莫斯科数学学会的会议上宣读,勃拉什曼是这个学会的创始人。
在大学的最后一年,切比雪夫写了一篇题为《方程根的计算》的论文,提出一种建立在反函数的级数展开式基础上的近似解法,从而获得系里该学年度的银质奖。
1841年春,切比雪夫毕业于莫斯科大学,开始攻读硕士学位。但是生活不是一帆风顺的。由于灾荒,他们家在卡卢加省的庄园破产了,父母不仅不能向他提供继续深造的费用,而且还要把两个未成年的弟弟交给他教育和抚养。切比雪夫靠着微薄的研究生津贴度日。五年过去了,他不仅以优异的成绩获得硕士学位,而且还把两个弟弟相继送进彼得堡炮兵学院。
小弟弟弗拉基米尔·里沃维奇(B.I. He6ume,1832-1905)是这个家族的又一骄傲,他后来成了炮兵学院的教授兼将军,在机械理论和武器制造方面颇有造诣,是第一个指出机械加工表面微震动原因的学者。他与哥哥始终保持着极亲密的关系,Π.Л.切比雪夫的第一个论文集,就是由他整理和出资刊行的。
当时数学界有两家权威的刊物,都叫《纯粹与应用数学杂志》,由于创办人的不同也有人把它们分别称为《格列尔杂志》和《刘维尔杂志》①。世界上任何一个有名望的数学家,都以能在这两家刊物上发表文章为荣耀。还在当研究生的切比雪夫,于1843、1844年相继在两家刊物上发表了论文,前一篇是关于多重积分的,后一篇是关于泰勒级数的收敛性的。这两项工作标志着他在经典分析领域已具备相当扎实的基础。但踌躇满志的切比雪夫锋芒一转,他要去啃概率论这个坚果了。
概率论是研究随机现象的数量规律的一门科学。它最初产生于推测赌博输赢的问题,后来逐渐被应用到人口统计、法律诉讼和保险等事业上,到法国数学家拉普拉斯(S.Laplace,1749—1827)出版《概率论的分析基础》一书的时候,这门学科已初具规模。但是,由于早期的某些研究者过分强调它在伦理科学中的作用和企图以此来阐明“隐蔽着的神的秩序”,也几乎断送了它作为一门精密科学的前途。
切比雪夫是在概率论门庭冷落的年代从事这门学问的。他一开始就抓住了古典概率论中具有基本意义的问题,即那些“几乎一定要发生的”事件的规律——大数定律。
历史上的第一个大数定律是由瑞士数学家雅各·贝努里(Jacob Bernoulli,1654-1705)提出来的,后来法国数学家泊松(B.Poisson,1781-1840)证明了一个类似而条件更宽的命题,除此之外在这方面没有什么进展。1845年,切比雪夫在其硕士论文《试论概率论的初等分析》中,借助很初等的工具——ln(1 x)的麦克劳林展开式,对贝努里大数定律作了精细的分析和严格的证明。次年,他又把结果拓广到泊松形式的大数定律。这年夏天,切比雪夫正式通过了论文答辩,获得硕士学位。他以精确的分析手段研究大数定律,不但使概率论脱去了神学的外衣,而且开始了研究方法上的一系列变革,从而把这门学科推进到现代化的门槛。
二十余年后,切比雪夫重新回到这一课题,在1867年发表的《论平均数》中进一步讨论了作为大数定律的极限值的平均数。1887年,他发表了更为重要的《关于概率的两个定理》,开始对中心极限定理进行研究。
在这一系列的研究中,他首先引出并倡导使用的随机变数,后来成了概率论与数学统计中首屈一指的概念。他创立的“矩方法”解决了许多困难的问题,直到今日仍被广泛应用。导致产生这一方法的,是他在1882年建立的一个著名不等式,这个今日冠以切比雪夫大名的不等式断言:若是一随机变量、a是其平均数、是的平均数,则对任何正数,使成立的概率不超过。这一关系后来成了一系列更为精确地估计概率的不等式的先导。切比雪夫的学生马尔科夫(A.A.Mapxor,1856-1922)后来对“矩方法”作了某些补充,圆满地解决了随机变量的和收敛正态的条件问题,另一个学生李雅普诺夫(A.M.JIxnyHoB,1857—1918)把“矩方法”发展为特征函数法,他的工作成了中心极限定理研究中的真正转折点。
切比雪夫还提出了估计中心极限定理中有关收敛速度的课题。他猜想:在一定条件下,有可能依照的方幂渐近展开独立随机变数和的分布函数,这里n是和中的项数。这一猜测,完全被后来的研究所证实和解决。本世纪四十年代,有人解决了收敛速度的一致估计问题,六十年代则有人从事分布函数的渐近展开。近年来,我国年轻一代的概率统计工作者,又把这些成果改进到更广泛的场合。
应该指出,切比雪夫所从事的大数定律和中心极限定理的研究,还是属于概率论的古典极限定理范畴。当时这门学科的逻辑基础尚未奠定,一些重要的理论工具如集合论、测度论也不具备,甚至概率自身的古典定义中也隐伏着循环推理的致命内伤,贝特朗悖论②又使几何概型陷入困窘的境地。切比雪夫正是在这种荆棘丛生、危机四伏的环境中开出一条新路的。他所完成的方法论方面的基本变革不仅提出了满足于严格证明的要求,而且能够随时精密地估计试验的结果,他引出的一系列基本概念和课题为俄国和后来苏联的数学家所继承和发展。从本世纪三十年代柯尔莫哥洛夫(A.H.Konxoropor,1903-)建立概率论的公理体系为标志,苏联在概率论领域获得了无可争辩的领先地位。第二代极限理论——无穷可分分布律的研究也出现在切比雪夫的故乡,经辛钦(A.H.XurqKn,1894-1959)、格涅坚科(B.B.Tneaerko,1911一)等人完善,成为古典极限定理在二十世纪抽枝发芽的繁茂大树。如果切比雪夫冥中有知,一定会含笑九泉的。
欧拉选集和数论
1846年,切比雪夫作出了一个对其日后科学生涯至为关键的选择,接受了彼得堡大学的助教职务。
经过一百多年的建设,彼得堡早已不象当年那样空旷荒凉。涅瓦河上架起了几十座铁桥,市区和彼得罗巴夫洛夫斯克要塞之间铺成了俄国唯一的一条铁路,凝聚着古典美和俄罗斯风格的海军大厦的尖顶直指苍穹,冬宫和夏园则堪与凡尔赛相媲美。然而它在文化教育上的地位还不能与故都相比。1804年彼得堡才有了一所国立师范,1819年改为彼得堡大学,其声名和设备都远远逊于莫斯科大学。在囿守传统的俄国知识分子眼里,彼得堡是军人和政客的天地,俄罗斯文化的精华还在昔日的都城莫斯科。
但是彼得堡大学有两位出类拔萃的数学教授,他们对年轻的切比雪夫具有难以抗拒的吸引力。
奥斯特洛格拉德斯基(M.B.Ocrporpaacxn8,1801-1862)在哈尔科夫大学读书时,由于反宗教的观点未能获得毕业证书。后来他到巴黎深造,亲承拉普拉斯、富里埃(J.Fourier,1763)--1830)、柯西(L、Cauchy,1789-1857)等大师的教诲,在理论力学,概率论与数论方面都有精湛研究,尤其擅长积分计算,关于体积分和面积分关系的著名公式就是他发现的。他也是一位优秀的教育家和组织者,写过不少数学教科书,1830年被选为彼得堡科学院院士。
布尼亚科夫斯基(B. 8. By8KOBCxB8,1804-1889)也是在巴黎学成后回国任教的,同样在1830年被选为科学院院士。此时他正在准备出版自己的《概率论的数学理论基础》,他对切比雪夫在硕士论文中表现出来的精确分析手法十分欣赏。在数论方面,他对叠合与二次互反律都有独到的研究。他热心地参加和主持教育改革委员会,对制定俄国中等和高等数学教育大纲和数学术语的规范化起了重要的作用。
在彼得堡大学的青年教师中,切比雪夫很快就显得鹤立鸡群。1847年春天,他在题为《关于用对数积分》的晋职报告中,彻底解决了奥斯特洛拉德斯基不久前才提出的一类无理函数的积分问题,他所得出的关于二项式微分式积分的条件和方法,今日已被写进任何一本数学分析教科书之中。在这一工作中,他也接触到了少年时代就为之神往的数论问题。然而更强烈的刺激还在后面。
切比雪夫到彼得堡来工作前两年,大数学家欧拉的曾外孙、身为科学院秘书的富斯(IⅡ.H. bycc,1798-1855),在科学院的档案中发现了大批欧拉生前未曾公开过的数学手稿,科学院决定立即组织人力编辑出版欧拉选集。布尼亚科夫斯基后来推荐切比雪夫担任数论部分的实际编辑工作。1849年,关于数论方面的欧拉选集在彼得堡正式出版。
正是在这件看来繁琐枯燥的工作中,切比雪夫体会到了科学巨人深邃的思想和高度的技巧结合起来的神奇与美妙。欧拉引入了一个ξ函数证明所有素数的倒数和发散,这实际上给出了素数有无穷多的又一个简单证明。少年时代的激情在他胸中重新涌起:ξ函数对于神秘的素数分布规律来说,也许正是那“芝麻——开门”的咒语。
素数分布的规律,这个数论中的基本问题,自欧几里得以来还没有什么实质性的进展。如果以表示不大于的素数的个数,所谓素数分布的问题就是要找出一个用来表示的的公式。法国数学家勒让德(A.M.Legendre,1752-1833)和高斯分别研究过400,000和3,000,000以内的素数表,猜测过关于的一些性质;前者认为,其中A=1.08366;后者断言与,的非常小,他们都猜测。最后这一猜测就是著名的素数定理,但是连高斯这样的巨匠也没能给出证明。
当时在德国,正由狄里克莱(P.L. Dirichlet,1805-1859)、稍后由黎曼(B.Riemann,1826—1866)领导着一场革新数论方法的运动。他们大力倡导在代数方法之外应用分析学的手段研究这门古老的学问。其实这种思想在欧拉的著作中已现端倪:他引入的ξ函数正是来自分析学的一个结果。因而兼具分析之长和谙熟欧拉思想的切比雪夫,在俄国成为这一场数论方法论革新运动的呼应者就毫不足奇了。
大约在编辑欧拉选集的同时,他就开始了对素数定理的研究。在两年多的时间里,他相继搞清了若干重要的问题:他指出勒让德公式中的最佳逼近值A不是1.08366而是1;他利用ξ函数证明了高斯的猜测与甚为接近;他给出了精确的估计式③。
所有这些成果,都被写进他的博士论文《论同余式》中。1849年5月27日,彼得堡大学为他举行了答辩,报告引起震动。他不但获得了博士学位,还被科学院授予最高的数学荣誉——杰米多夫奖。
第二年,他又向科学院提交了另一篇更重要的数论论文《论素数》,在进一步完善上述结果的同时,他又引入的两个函数和,它们在数论中有重要作用,如今被人称为切比雪夫函数。另外,他在该文中还顺便解决了关于素数分布规律的又一猜测:对于任何大于的数来说,在与之间至少存在一个素数。这一猜测是法国数学家贝特朗(就是上一节所提到的制造了一个几何概型方面的悖论的人)在1845年通过观察素数表作出的。但是无论是他本人还是其他的数学家,都未能对这一貌似简单其实深刻的命题给出理论证明。
这两篇论文奠立了切比雪夫在科学界的地位,也标志着俄国数学家在数论领域开始走向了世界前列。若干年后,它们被不断地翻译成各国文字,成为解析数论方面不朽的经典文献。
瓦特连杆和函数逼近论
1852年7月,切比雪夫接受了一项使命,到西欧进行数学和技术的综合考察。如同当年的彼得大帝一样,他怀着新奇和激奋的心情踏上了异国的土地。然而他已无需忍受漫长道路上的颠簸和驿站里臭虫的袭扰,蒸汽机车代替了四轮马车。世界像列车一样地向前奔驰,他在工业革命的发源地获得了新的创造灵感。
当车轮与铁轨的撞击在夜空发出催人入眠的单调声响时,切比雪夫却在为一个崭新的数学问题苦思冥想:如何描述蒸汽机的关键部件瓦特连杆的运动,以便建立一种直动与转动互换的理论和算法?更一般地讲,是否存在着一种数学工具、可以把复杂的机械运动用数学形式表示出来?
在大约半年的时间里,他一有空就钻进技术博物馆,观察和分析各种各样的机械。在巨大的荷兰风车旁,他像一个孩子看到了新奇的玩具一样地流连忘返。在一家大型机器厂里,他满手油污,把传动齿轮拆了又装、装了又拆。他自幼就对机械有一种异乎寻常的热情,在莫斯科大学曾选读过机械工程课,就在出国之前,他还兼任过彼得堡大学应用知识系(准工程系)的应用力学课讲师。这个当年在磨坊里消磨时光的跛腿少年和未来俄国数学王国里的彼得大帝,此时正在构思着函数逼近论的基本思想。
他设想有一种理想的机器,当它运转时其上的某一点画出一条理想的曲线;但工程师设计出来的机器往往只能得到一条近似的曲线g,就象瓦特连杆只能近似地将圆变为直线一样,再假定全部零件的参数、、。完全确定了机器,那么就表示实际机器上相应点的运动曲线。切比雪夫提出用
如果上述曲线由一个多项式表示,那么使得设计标尺达到最小的就叫最佳逼近多项式。切比雪夫论证了最佳逼近多项式的一系列性质,引入了切比雪夫交错组和符号判别法,证明了具有切比雪夫交错组的多项式即最佳逼近多项式。不仅如此,他还找到了这样一个与零偏差最小的最佳逼近多项式。为了纪念他所作出的这些奠基性的工作,现在人们就把叫做切比雪夫多项式,把若干关于最佳一致逼近的定理叫做切比雪夫定理,把最佳一致逼近叫做切比雪夫逼近。
回国以后,切比雪夫很快就向科学院提交了这方面的研究报告,第一篇关于函数逼近论的论文于1854年正式发表。从此他在相当长的一段时期内致力于这一分析学的未知领域的探索,数十年内硕果累累。除了一致逼近之外,他又研究了平方逼近、三角多项式逼近和有理函数逼近等课题。这些成果又与多项式理论、正交理论、矩阵论、内插法、近似积分、误差估计等内容密切联系,极大地丰富了十九世纪分析学的内容。
这一开拓性的工作很快就引起了世人的注意。德国数学家外尔斯特拉斯(K.Weierstrass,1815-1897)、李普希茨(R. Lipschitz,1832-1903)以及切比雪夫的门生科尔金(A. H.KopKnH.1837-1908)、佐洛塔廖夫(E.H.3ozorapen,1847-1878)等人相继为这门崭新的数学分支做出了重要贡献。进入本世纪以来,以法国数学家波莱尔(E.Borel,1871—1956)和苏联数学家伯恩施坦(C.H.Bepaurean,1880-1968)为代表的现代逼近理论大放异彩,成为数学园地中一枝奇艳的花朵。
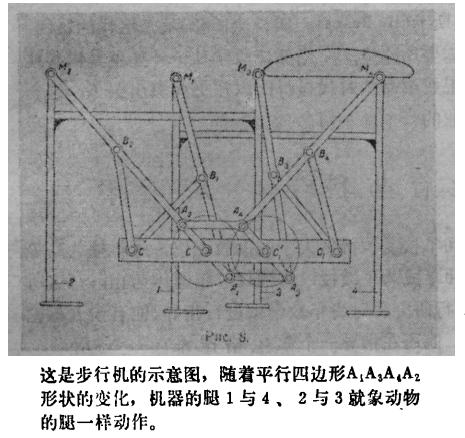
函数逼近论的诞生是数学来源于实践的一个有力证明,下一步是实践向数学索取报酬了。的确,由于有了先进的数学工具,切比雪夫得以建立许多关于机器设计的理论和算法,例如直动机的理论、连续运动变为间断运动的理论、最简平行四边形法则、绞链杠杆体系成为机械的条件、三绞链四环节连杆的运动定理、离心控制器的原理等等。依靠这些理论和算法,切比雪夫亲自设计和制造新的机器。据统计,他一生共设计了四十多种机器和八十多种这些机器的变种。其中有精巧的步行机,可以维妙维肖地模仿动物行走的动作,有奇特的划船机,可以完成船桨不断变换角度的复杂运动,有别具一格的曲尺和曲线规,可以量度圆弧的曲率和绘制直径很大的圆弧;还有压力机、筛分机、选种机、自动椅以及大量的计算机。他的许多新发明曾在1878年的巴黎博览会和1893年的芝加哥博览会上展出,引起各界人士的极大兴趣。现在苏联科学院数学研究所、莫斯科历史博物馆和巴黎艺术学院都藏有若干切比雪夫发明的机器或仪器。
理论联系实际,不仅体现在切比雪夫对函数逼近论与机器设计的研究中,而且可以说是贯穿他全部科学工作的一个鲜明特点。从西欧出访归来不久,他就被选为彼得堡科学院应用数学部的主席,这个位置直到他去世后才由李雅普诺夫接任。1852—1856年他受聘在亚历山大学院(在今高尔基城)讲授应用力学,同时他与莫斯科技术学院(现鲍莫技术学院)保持着密切联系。
1856年,切比雪夫被任命为炮兵委员会的成员,积极参与制定了革新俄军炮兵装备和技术的计划。1867年,他提出了一个计算圆形炮弹射程的公式,立即为军队所采用。他关于插值理论和二次型的数学研究,就起因于分析弹着点试验数据和弹道计算的需要。


1856年,彼得堡大学举行一年一度的教授联席会议时,切比雪夫作了《论地图制法》的著名报告。他说:“理论与实践接近,便产生最好的结果。受益的不仅是实践方面,就是理论科学本身也将受刺激而发展起来,因为前者替它揭示了新的研究对象或已知对象的新侧面。”正是在这篇演讲中,他提出了减少投影误差的详尽讨论。
1878年,切比雪夫应邀出席法兰西科学院第七次年会,在他提交的四篇论文中竟有一篇名为《论服装裁剪》,文章提出了合理用料的数学解,引起了学者们的很大兴趣。回到彼得堡后,他还亲自跑到裁缝们那里去,指导他们合理用料的方法。这一研究进一步启发了他在曲面论方面的创造灵感,他接着考察了一种具有平行网格的“布”包裹曲面的问题。“切比雪夫网”今日已成了微分几何中的一个术语。
尽管切比雪夫是如此的多才多艺,但他从不把已经取得的成就归于天赋。在去世前不久,有一次他对一个学生瓦西里耶夫(A.B. Bacxxzea,1853-1929)半开玩笑地谈起了对数学发展的看法,他说,“早先人们只知道数学发展有两个阶段:在第一个阶段里,数学是由神建立的,像德罗斯祭坛的故事就说明如此④;在第二个阶段里,数学是由一些半人半神所建立的,费马(P.Fermat,1601-1665)、帕斯卡(B.Pascal, 1623-1662)就是这样的怪物。现在我们到了第三个阶段;数学为社会实际需要所建立。”当然,数学从一开始就是由实践所决定的,切比雪夫要强调的是这一观念在工业革命的时代显得比以往更为突出罢了,这一朴素的唯物主义思想正是他毕生从事科学事业的一个基本信念。
献身于教育与科学
切比雪夫是一个杰出的教育家。他自1846年接受彼得堡大学的助教职位、次年擢为高等代数和数论的讲师、1850年升为副教授、1860年成为正教授,直到1882年退休为止,在这所大学执鞭达三十五年。退休之后,他还继续进行研究和对青年数学家进行指导。他有十五篇论文是在1882年以后发表的,直到临终前几天,他还在指导一个学生格拉维(Л.A. Tpase,1863-1939)将自己不久前刚获得的平面曲线弧长的近似公式推广到空间的工作。
三十五年间,他教过十余门课程,遍及数论、高等代数、积分运算、椭圆函数、有限差分、概率论、机械工程、分析力学、傅里叶级数和函数逼近论等分支。他的讲课深受学生们的欢迎,他绝不进行经院式的长篇说教,而总是力求阐明最基本的概念和对有关背景及方法给出精辟的评论。李雅普诺夫说:“他在课堂上附带给出的一个评论,往往恰与听讲者冥冥中苦思的某个问题有关,因为他早就在留意学生们的思想活动。因而,这种讲课具有强烈的感染力,每堂课都能使人获得宝贵的知识。”
1872年,切比雪夫在彼得堡大学任教二十五周年,为了表彰他为教育事业作出的贡献,彼得堡大学授予他功勋教授的称号。
从1856年起,切比雪夫还参加了教育部属下的全俄中等教育改革委员会,和奥斯特洛格拉德斯基、布尼亚科夫斯基等人一起,草拟中学教学大纲、制定新的教材。据统计,经切比雪夫审阅的各种数学、物理和天文学教材达二百余种。这说明他不仅关心高级科学人才的培养,也致力于整个民族科学文化的普及与提高。
1853年,切比雪夫被选为彼得堡皇家科学院的候补院士,同时兼任应用数学部的主席,1856年成为副院士,1859年成为正院士,这一年他不过三十八岁。国外的荣誉也纷至沓来:1860年切比雪夫当选为法兰西科学院的通讯院士,1871年为柏林皇家科学院的通讯院士,1877年为伦敦皇家学会所接受,1880年和1893年则分别为意大利和瑞典皇家科学院所接受。同时他也是全俄罗斯所有大学的荣誉成员和彼得堡炮兵科学院的成员。
在所有的外国科学团体中,切比雪夫与法国科学院的交往是最为密切的了。他曾三次赴巴黎出席该院的年会,每次都提交三、四篇论文。他与法国数学家卡塔兰(E. C.Catalan,1814-1894)、达布(G. Darboux,1842-1917)、刘维尔以及德国数学家克罗内克(L.Kronecker, 1823-1891)、外尔斯特拉斯保持着经常性的学术联系。在他死后的遗物中,还发现了他同埃尔米特(C. Hermite,1822-1901)、柯西、克雷蒙纳(L.Cremona,1830-1903)、萨律(P.F.Sarrus,1789—1861)等人的来往信件。他一生曾先后六次出国考察、访问或出席学术会议,这些广泛的国际交流,不但对他自己的研究起了推动作用,而且为俄国数学界在国外赢得了声誉。
切比雪夫也以充沛的精力和饱满的热情活跃在国内各种科学团体和会议上。他是彼得堡和莫斯科两地数学会的热心赞助者。他发起召开的全俄自然科学家和医生代表大会,对于促进俄国科学界之间的相互了解和扩大科学在民众中的影响起到了历史性的作用,也加速了彼得堡数学学派的形成。
在历次会议上,切比雪夫报告了一系列精彩的论文,同时他总是及时地发现和扶植年轻的科学人才,他把这种盛会看成是培养新一代科学家的大课堂。
1869年,在莫斯科召开的第二次代表大会上,工程师马耶夫斯基(H. B.Maneacxn.1823—1892)报告了关于用实验方法得到的椭圆形炮弹飞行中阻力问题的结果。可惜他只讨论了一种极特殊的情况,而一般情况的理论分析对于这位工程师来说是非常困难的。在切比雪夫的细心指导下,他后来终于获得了一般的计算公式,成为当时国际上最好的结果。
两年后的第三次代表大会上,切比雪夫碰到了两个年轻的数学家;叶尔马可夫(B.II.Epaaxoa,1845—1922)和布加耶夫(H.B.Byraen,1837—1903)。前者发现了一种级数 收敛判别法则,其简洁和有效都在当时已知的其它判别法则之上。切比雪夫高兴地肯定了这一成果,并进一步提出它与微分方程特解判别法之间的联系,为更深入的研究指明了方向。后者关于数值导数的应用的文章也有新意,但处理数值函数的方法过于繁复,切比雪夫当年的论文★论素数》恰好解决过类似问题。在他的指点下,布加耶夫茅塞顿开。
切比雪夫关怀青年学者的事例莫过于他对女数学家柯瓦列夫斯卡娅(C. B.Korazeackan,1850—1891)的帮助与支持了。柯瓦列夫斯卡娅是一个传奇性的女性,她为了获得在俄国不可能得到的接受高等教育的权利,在十八岁那里从优裕的家庭出走,与人缔结形式婚约到德国上大学。后来她成为外尔斯特拉斯的入室弟子,1874年成为世界 上 第一个女数学博士。1879年,柯瓦列夫斯卡娅在第六次自然科学家和医生代表大会上曾作《关于阿贝尔积分》的报告。两年后在第七次大会上,她又报告了关于晶体中光线折射现象的结果。1888年又由于成功地解决了刚体绕定点转动问题荣获法兰西科学院的布尔丁大奖,成为轰动一时的新闻。但是对于这位给俄国带来世界声誉的女学者,愚昧的沙皇政府却以种种借口阻挠其回国工作,因为她不但是一个女人,而且具有强烈的民主主义倾向。这时,切比雪夫挺身而出,与布尼亚科夫斯基等人联名向科学院推荐她为通讯院士。这一动议在1889年11月16日的院务会议上引起了激烈争论,最后以二十票对六票获得通过。
有趣的是,切比雪夫尽管对柯瓦列夫斯卡娅给予巨大的支持,他们在学术上却各持一端,每次见面都要争得面红耳赤。这种争论,实际上是以外尔斯特拉斯为首的柏林数学家同以切比雪夫为代表的彼得堡数学家之间分歧的表露。切比雪夫认为外尔斯特拉斯只是抽象地提出问题,把积分从一种形式变换成另一种形式,最后并不能具体地解决问题;外尔斯特拉斯则批评切比雪夫忽略对一般规律的研究和陈述的规范化。
应该承认,外尔斯特拉斯的批评是不无道理的。在函数逼近论的研究中,由于切比雪夫更多地把注意力放在找出具体的最佳逼近多项式上,而忽略了这种多项式是否一定存在的问题,正是外尔斯特拉斯后来证明了其存在性。联系到切比雪夫在素数定理的工作中也留下了一个存在性的尾巴,可以看出他在研究工作中相对薄弱的一个环节;就是过分强调实用性而不够注意某些存在性问题。否则,以他的才力和知识面而言,定会取得更为辉煌的成就。这也是值得我们今日在处理理论与实践关系时引以为鉴的。
第六次代表大会是俄国数学界的空前盛会,一大批新人崭露头角,他们之中有的是彼得堡大学的毕业生,有的是得益于切比雪夫教诲的其他地方的青年学者,一时风云际会、群贤一堂。看到自己培养出来的学生登上科学讲坛,切比雪夫感到由衷的喜悦与骄傲。
切比雪夫终身未娶,日常生活也十分简朴,他的一点积蓄全部用来买书和制造机器的设备。每逢假日余暇,他也乐于同侄儿女们玩上一阵,但他最大的乐趣还是与青年人谈论数学。1894年11月底,他的腿疾突然加重,思维也出现障碍,但他还是要求自己的研究生按时前来讨论问题。1894年12月8日上午九时,这位令人尊敬的老人在自己的书桌前溘然长逝。他既无子女、也无金钱,但他给全人类留下了一笔不可估价的遗产——一个辉煌的学派。
彼得堡数学学派
十九世纪数学的一个特点是学派的兴起。
诞生在资产阶级大革命风暴中的法兰西学派仍然雄踞着数坛,他们勇于抛弃旧的框框,极富创造精神,在函数论、数学物理、群论和新的综合几何学方面占有巨大优势。具有哲学传统的德国人特别注意数学的基础问题,“算术化”成了柏林学派的重要特征。另外,德国数学家不像法国同行那样都集中在首都,波恩、莱比锡、哥廷根都有知名学者;尤其是最后这座城市,不久就要取代巴黎成为数学的耶路撒冷。英国人也开始从固步自封中觉醒,1812年在牛顿的母校有一群年轻人竟敢冒着亵渎神圣的罪名去推广大陆的微积分记号⑤,这一世纪中他们在代数方面获得了巨大的成就。在文艺复兴的故乡,以几何与拓扑为突破口的新意大利学派正在成长……
当然,任何企图用三言两语来说明一个学派特点的作法都难免失于偏颇。衡量一个学派是否成熟,起码应从以下三个方面进行详细考察,这就是:(1)是否拥有德高望重的领袖和人才济济的阵容?(2)是否具有开拓性的工作和影响深远的成果?(3)是否形成了独特的学术风格?
按照沃尔特拉(V.Volterra,1860-1940)的意见,新意大利学派诞生于1858年布廖斯奇(E. Brioschi,1824—1897)、贝蒂(E.Betti,1823-1892)到德、法两国的工作旅行⑥。但是在俄国历史上却很难找到一个事件作为彼得堡学派呱呱落地的标志。它可以远溯到欧拉的应召前来,与布尼亚科夫斯基和奥斯特洛格拉德斯基留法回国从事教育也不无关系,但最终它是伴随着切比雪夫几十年舌耕笔耘的生涯成长壮大的,到十九世纪末俄国终于形成了一支可观的数学攻坚力量,切比雪夫是这一派学人当之无愧的领袖。
马尔科夫和李雅普诺夫可谓切比雪夫的左膀右臂,他们分别于1878和1880年毕业于彼得堡大学数学系。马尔科夫在毕业的当年即以连分数解微分方程获金质奖,一生著述七十余种。他在概率论中除了发展“矩方法”、扩大了极限定理的应用范围外,还开创了一种无后效性随机过程的研究,被人称为马尔科夫过程,在物理、化学、生命过程和公用事业中都得到广泛的应用。李雅普诺夫在数学物理中钻研位势理论,开拓了微分方程稳定性理论的方向。他后来到哈尔科夫任教,使那里成为俄国又一个数学中心。
科尔金和佐洛塔廖夫在函数通近论方面的贡献我们已提到。他们分别是彼得堡大学1858年和1867年的毕业生,还曾合作解决了含五个变量的正定二次型的最小值问题,又都擅长代数与数论。
索霍茨基(IO.B. Coxouxn,1842—1929),1866年毕业,发现了复变函数论中的索霍茨基一外尔斯特拉斯定理,弄清了本性奇点邻域内的函数质谈,还在极一般的条件下研究了柯西型积分的边值问题。
波瑟(K.A.Iocce,1847-1928),1868年毕业,擅长于数学分析,在正交函数和定积分的计算方面有特殊的造诣。
格拉维,1885年毕业,博士论文讨论制图投影,找到了球在平面上的所有可能的等效投影,证明了切比雪夫提出的关于在地图上表示最佳投影的定理。以后专攻代数和群论,成为俄国在代数领域的开创者。
伏罗诺伊(r.@.Boponon,1868-1908),1889年毕业,博士论文是《连分数算法的一个总结》,后与德国著名数学家闵可夫斯基(H、Minkowski,1864-1909)共同创立数的几何学,在多角形理论和级数求和方面的工作也很出名。
许多并非彼得堡大学出身的青年也深受切比雪夫的影响。交通道路学校的沙图诺夫斯基(C.H. MaTyHoBcKni,1859—1929)为了听切比雪夫的课,特意到彼得堡大学做旁听生,后来成了敖德萨数学学派的先驱。海洋学院的克雷洛夫(A.H.Kpaaoa,1863-1945)利用切比雪夫提出的近似公式,得到船舶设计方面的重要结果。莫斯科大学的茹可夫斯基(H.E.Ky-xoecxxa, 1847—1921)在解析函数和偏微分方程方面曾得益于切比雪夫的指教,他后来成了现代流体力学的创始人和俄国航空之父。斯捷克洛夫(B.A.CrexoB,1864-1926)在哈尔科夫跟随李雅普诺夫学习,在函数论、微分方程、数学物理方面都有出色贡献,并成为彼得堡学派在十月革命以后的重要传人。
正是这些奋发有为的后起之秀们,把切比雪夫在概率论、数论和函数逼近论中开创的事业继承下来,并将俄国数学在这三个领域中的优势一直保持到本世纪,又与微分方程、数理统计、函数构造、泛函分析、近似计算等分支纵横交错、左勾右连,成为这一学派大显身手的广阔天地。
那么,彼得堡学派独特的风格是什么呢?我们大致可以归纳成如下的四点:
-
重视基础理论、善于以经典课题为突破口。
切比雪夫从经典分析起家,在多重积分和泰勒级数方面做了一些工作后转到概率论,并在一开始就抓住了当时这门学科中最本质的内容大数定律和中心极限定理。由于熟悉欧拉等前代大师的著作,他在数论研究中能够果断地选择意义重大的素数分布问题作攻坚对象。他对逼近论的研究则是建立在对实数理论的严密逻辑基础深刻的认识上。这种重视基础理论和经典课题的作风在他的后继者们那里得到了进一步地发扬光大。维诺格拉多夫(H.M.Bna-orpanon,1891—1983)首创三角和方法研究哥德巴赫猜想,盖尔方德(A.O.Tenbpaxa,1906-1968)解决希尔伯特(D.Hilbert,1862-1943)第七问题,柯尔莫哥洛夫奠立概率论的公理化基础等事例,都可以说是这一传统的突出表现。
2.理论联系实际。
这是任何一个有成就的数学学派都具有的特点,只不过在切比雪夫和他的学生们那里更为明显罢了,函数逼近论和机器设计的相得益彰就是最有说服力的例证。切比雪大对于有关的数学结果,总是追求精确的表达式,实在不能得出的则给出近似公式和误差估计。著名的切比雪夫不等式是在看不出实际用途的数论领域中推出的,如今成了概率论中不可缺少的工具。他交给李雅普诺夫的旋转液团在平衡状态下形状的课题,导致了运动稳定性理论的建立。
3.擅长运用初等工具建立高深的结果。
从步入科学殿堂之初,切比雪夫的工作就显示了简单化和初等化的风格。幂级数和连分数在他手中运用自如,常常在深奥莫测的数学土壤上结出令人惊诧的奇花异果。马尔科夫、伏罗诺伊以及后来的辛钦应用连分数于差分理论和复变函数,获得许多有意义的结果。这种本领是建立在扎实的基本功和敏锐的洞察力的基础上的。
4.以大学为阵地,科研与教学密切结合。
像许多优秀的数学学派一样,彼得堡学派是深深地扎根在大学的沃土上的。切比雪夫从年轻的大学生那里汲取创造的灵感,学生们则从他那里得到启发。切比雪夫和他的弟子们从不把教学看成是科研的负担,而是力图在课堂上向学生们阐明最新的科学思想。斯捷克洛夫对李雅普诺夫的第一堂课有过生动的描述:“这一位与我们班上同学中差不多同年的青年人··…在一个钟头内征服了这批怀有偏见的听众。”⑦而根据李雅普诺夫当年的听课笔记整理的切比雪夫的概率论讲义,出版后成了这门学科的重要文献。
十月革命以后,以斯捷克洛夫为首的一批数学家响应列宁的号召,积极拥护新生的苏维埃政权,并团结留在国内的著名科学家组成了莫斯科数学物理研究所。后来该所一分为二,数学研究所即以斯捷克洛夫命名。随着苏维埃政权的巩固与成长,一批优秀的数学家逐渐集中到该所和莫斯科大学来,因此出现了莫斯科学派的说法,它与彼得堡学派是一脉相承的。除此之外,在哈尔科夫、基辅、喀山、敖德萨、梯比里斯等城市也相继出现了数学中心,列宁格勒大学(原彼得堡大学)则继续不断地培养出第一流的数学人才。今日苏联数学界的头面人物,不管其工作基地在哪个加盟共和国哪个城市,他们都以能被称为彼得堡学派和切比雪夫的继承人为无上的荣耀。
上个世纪后半叶,切比雪夫和他的学生们以坚韧不拔的精神和勇攀高峰的气概,终于使俄国数学从一穷二白的境地中挣脱出来,并在若干领域内走到了世界的前列。考察切比雪夫和彼得堡学派的历史,对于我们当前学习和引进外国的先进科学技术来实现科学技术现代化,对于我们在数学领域选择突破口、充分发挥自己的优势,创立一个有特色的中国数学学派无疑是有意义的。
注释:
①分别由德国人格列尔(L. Grelle,1780—1855)于1826年、法国人刘维尔(J. Liouville,1809-1882)于1836年所创办。
②贝特朗(J.Bertrand,1822—1900)是法国数学家,他提出的在圆内作弦、使其长超过内接等边三角形边长的概率问题,从不同的思考角度出发可以得到三种互相矛盾的结果。
③1896年,法国数学家哈达马(J.lladamard,1865—1963)把欧拉和切比夫应用在实数范围的ξ函数推广到复数领域,用复变量的整函数理论证明了极限的存在性,从而最终完满地证明了素数定理。
④相传公元前五世纪,古希腊德罗斯岛盛疫流行,人们求告于阿波罗神消灾除难,祭司借神之口说,“尔等须把神殿前的立方体祭坛扩充一倍。”这就是有名的“倍立方”问题,它与“三分角”、“化翻为方”一起,成为古希腊数学史上著名的三大作图难题,直到十七世纪以后才被人证明为不可解的。
⑤指剑桥大学的皮考克(C.Peacock,1791-1856)、拜比吉(C. Babbage,1792—1871)、小赫歌耳(J. F. W.Hershel,1792—1871)等人发起的分析学会和推广莱布尼茨(W.Leibniz,1646-1716)符号系统的运动。由于类、德数学界长期以来为微积分的发明权争吵不休所以这一运动当时遭到保守势力的强烈攻击,后来终于获得胜利。
⑥布塞斯奇、贝蒂都是意大利学派的创始人,这一学派几乎与彼得堡学派同时形成,其代表人物还有克雷蒙纳、贝特拉米(E. Beltrami,1835—1900),沃尔特拉则是这一学派的第二代数学家。
⑦B.N.斯米尔诺夫:“亚历山大·米哈依罗维奇·李雅普诺夫传略”,见《中学数学》第二期,1957年。
主要参考文献
[1] B. E. Mpyaxaxos: M. I. He6umen, yeust Ieraror, Mocxsa (1950, 1964).
[2] Ch. C. Gillispie 主编:Dictionary of Scientific Biography, New York (1971), Vol. Ⅲ, pp. 222-232.
[3] bonbman CoBeTckaR3HuXKnoneAg8,MocKBa(1978).
[4] A. A. 3Bopuxn 主编:Baorpawqeckn Cnosap learexet EcTeCTBO3HAHNA H TexHax, Mockaa(1958,1959).
[5]A. A.亚历山大洛夫等主编;《数学——它的内容、方法和意义》中译本,第二卷,科学出版社,1963年。






