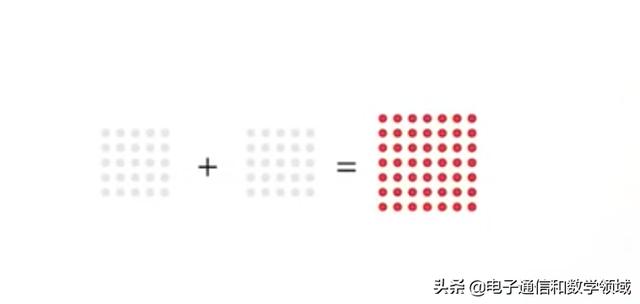
如果你是一个舞蹈家,想要编排一种舞蹈,让如下图两个正方形汇聚成一个大正方形,所以你能想象两个正方形到处移动,最后他们俩汇聚到一起,你就能看到一个大正方形的阵列。
这个想法很美好,能不能做到呢?首先我们要搞明白这个正方形要多大,所以我们可以一开始设计一个很小的正方形
这里是2X2的方阵,有没有用呢,我们看4个人的阵列 4个人的阵列,形成共计8个人的阵列,但我们需要一个平方数,所以这不会奏效。

那么下一个方阵3X3,9个人的阵列 9个人的阵列,形成共计18个人的阵列,这也不是一个平方数,所以也无法奏效。

继续方阵4X4,16个人的阵列 16个人的阵列,形成共计32个人的阵列,这也不是一个平方数,所以也无法奏效。

那么方阵5X5,25个人的阵列 25个人的阵列,形成共计50个人的阵列,其实很接近,比49多了1,不管怎样,我们继续

按上述规律眼看越来越接近,最终我们应该能找到吧,这个已经很接近了,来一个更大的方阵,12X12的,实际上这个也不会奏效

但最终总能奏效的,而且我想要小一些,12的平方是144,乘以2就是288,而17的平方是289,所以就相差了1
但这足以向我们展示接下来将要发生的事情了,我们就先不去担心能否找到合适的例子了,我们要上述方阵汇聚到一起,看看会发生什么
我们假设这是找到的能满足的最小的例子,让我们移动这些正方形,这个只是一个背景,让我们好看清楚它们是如何汇聚的,蓝色的点会匹配这里的网格。


现在我们就分别从左和右让两个方阵汇聚,如下图,它们会在中间有重叠部分

这虽然算是个小问题,但是不要紧,只是有些人站在了他们战友的肩膀上,对吧,所以红色点区域都有两倍的人,在这个大方块里,灰色方块是没有人站着,蓝色区域只有一个人站着
如果单独看这些站在肩膀上的人(红色方块)它们应该能填充灰色空白的地方,因为无论如何我们总是要填满所有点,意思就是说:红色方阵的大小正好就是灰色的两个小的方阵之和
这就是本篇的主题,但是有一件非常奇怪的事情,我们一开始假设这是最小的例子,两个小的方阵能汇聚成为一个大方阵,但我们发现了更小的,这怎么可能呢?因为我们有发现了更小的方阵

你可以想破脑袋,但是对于合格悖论的唯一解释,就是不存在最下的方阵,因为如果有一个最小的,就不能有更小的了,我们一开始假设我们能找到最小的例子,但是这个悖论告诉我们不存在最小的例子

所以结论就是,无法让两个一样的方阵汇成大的方阵,这就是我们的证明
实际上在数学中这个方法叫做反证法,你假设某个结论是正确的,然后根据你的逻辑推理,直到出现一些不可能的事情,最终说明开始那个假设就是不可能的

我们也能用数学语言去描述它,或者从代数学角度
两个整数的平方和不可能等于某个整数的平方,如下这个式子得意思就是根号2无法写成整数除以整数的形式

也就是说根号2是无理数,所以方阵的例子得出根号2是无理数。
,