译者:刘鸿(lewis2012)审校:王玥亭(玥亭)
介绍
向量是具有大小和方向的实体。向量由分量组成。这些分量中的每一个表示沿着对应轴的位移。例如,表示为(2,3,1)的向量表示距离原点沿x轴两个单位的位移; 沿y轴有三个单位的位移; 沿着z轴的一个单位的位移。
向量之间可以进行加减运算。向量可以相乘以或除以一个标量。然而,与实数乘法不同,向量不能在它们之间相乘,但是存在两种特殊类型的向量乘法:向量点乘和向量叉乘。
在本节中,将学习计算机图形学中最常用的向量操作。将学习如何加减向量,如何乘以除以标量,如何计算向量点积和叉积。
向量
向量由N个分量组成。分量的数量决定了向量的维度。三维向量包含定义沿着x,y和z轴的三个分量。在数学上,三维向量定义为:

形象地,具有沿着x轴4个单位位移和沿y轴3个单位位移的二维向量u表示如下:
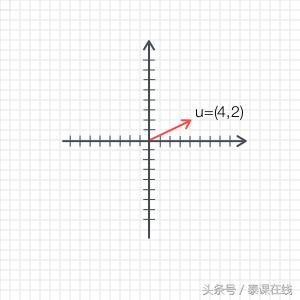
加/减运算
加法运算
在向量相加法中,每个向量分量被单独地添加到第二向量中对应分量。向量加法在数学上表示为:

例如,添加两个三维向量如下:

形象地,向量加法表示如下:

减法运算
在向量减法中,向量的分量彼此相减。向量减法在数学上表示为:

例如,两个三维向量相减如下表示:

标量乘法/除法运算
在几何上,将向量与标量相乘来修改向量的长度。将向量除以标量具有相反的效果。要将向量乘以标量,只需将每个分量乘以标量即可。注意,将向量乘以正标量仅影响其大小。然而,将向量乘以一个负标量,将会影响向量的大小也会反转向量的方向。标量乘法在数学上表示为:

例如,将向量缩放3倍的过程如下:

形象地,向量标量乘法表示如下:

向量乘积
与实数不同,向量不具有单个乘法运算。他们有两种不同类型的乘操作; 向量点积和向量叉积。向量点积产生标量,并且主要用于确定向量之间的角度。向量叉积产生垂直于被乘数和乘数向量的第三个向量。
向量点积
点积是计算两个向量之间的角度的向量操作。点积以两种不同的方式计算。
方式1:

在上面的等式中,关于向量之间的角度的信息丢失。然而,该方程的结果可以告诉我们每个向量的方向。例如,如果点积等于1,则意味着两个向量具有相同的方向。如果点积是0,则意味着两个向量彼此垂直。最后,如果点积是-1,则意味着两个向量都朝向相反方向。
方法2:
如果我们有兴趣寻找两个向量之间的角度,可以使用下面的点积方程。

向量叉积
两个向量产生一个平面。向量叉积运算产生垂直于两个向量的向量。两个向量的叉积计算如下:
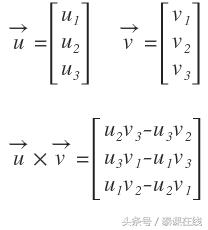
重要的是要记住,向量叉积只能用三维向量计算。如果向量存在于二维空间中,并且需要叉积,则向量必须转换为三维向量。
向量的大小
向量大小表示矢量的长度。向量的长度计算如下:
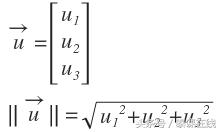
例如,向量u的大小如下:

形象地,向量的大小是在下面的图像中形成的三角形的斜边:

单位向量
计算机图形学中一个非常有用的概念是所谓的单位向量。单位向量是长度为一个单位的向量。将非单位向量转换为单位向量的过程称为归一化。为了归一化向量,每个分量除以向量的长度。数学上是这样的:

向量u的归一化如下:

【版权声明】
原文作者未做权利声明,视为共享知识产权进入公共领域,自动获得授权。
,




