毫米波雷达的优点
毫米波(mmWave)雷达是一类使用短波长电磁波的特殊雷达,其发射波长为毫米量级的信号。电磁频谱如下图所示,毫米波波长被视为短波长。

短波长的优势之一就是处理毫米波信号所需的系统组件(如天线)的尺寸很小,可将用于发送(TX)和接收(RX)的射频(RF)组件,时钟模拟组件,还有模数转换器(ADC)、微控制器(MCU)和数字信号处理器(DSP)等数字器件集成分布,降低功耗和系统总成本。
短波长的另一项优势是高准确度。工作频率为76~81GHz(对应波长约为4mm)的毫米波系统将能够检测小至零点几毫米的移动。
但集成分布带来的复杂性和雷达自身的高频率要求使得系统设计颇具挑战性。
线性调频连续波(FMCW)雷达是连续波雷达的一种特殊类型,相对于简单连续波(CW)雷达,通过对发射信号的频率调制(或相位调制)来改变其工作频率。
通过对工作频率(或相位)的测量来实现对目标信息的探测。接下来我们将详细介绍线性调频连续波雷达。
一、距离估计FMCW雷达基本原理这里介绍的FMCW雷达系统所用信号的频率随时间变化呈线性升高。下图以幅度(振幅)相对时间的形式,展示线性调频连续波信号。
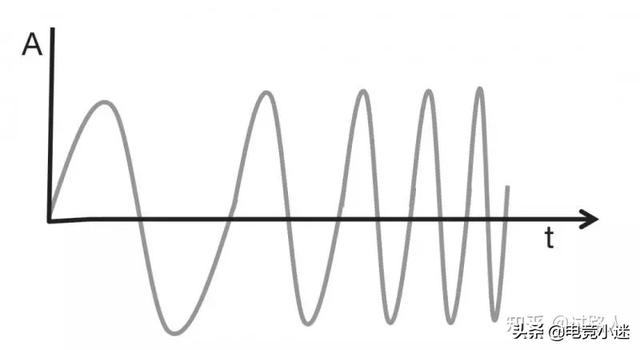
下图为同一个线性调频连续波信号(以频率相对于时间的形式)。该线性调频信号具有起始频率、带宽和持续时间。该线性调频信号的斜率表示频率的变化率。图中,,,,。

下图为FMCW雷达主射频组件的简化框图。

该雷达的工作原理如下:1、合成器生成一个线性调频信号;2、该线性调频信号由发射天线(TX 天线)发射;3、该线性调频脉冲经物体反射生成一个由接收天线(RX 天线)接收的反射线性调频信号;4、“混频器”将RX信号和TX信号合并到一起,生成一个中频 (IF) 信号。混频器混频器是一个电子器件,其可将两个信号合并到一起生成一个具有新频率的新信号。对于两个正弦输入和:
其输出信号的瞬时频率,等于两个输入正弦函数的瞬时频率之差。输出信号的相位等于两个输入信号的相位之差:
中频信号下图中的图(a)为针对单个静态物体的TX和RX线性调频脉冲的时间-频率波形图。则该RX的线性调频信号是TX线性调频信号的延时副本。

从发射信号起到接收到回波的时间为
其中是雷达天线与被检测目标的距离,是光速。混频器的输出IF信号为将两信号重合区(即图(a)中垂直虚线之间的时段)内的两信号相减即可。这两条线之间的距离是固定的,这表示IF信号是一个频率恒定的单音信号,且该恒定频率为。故雷达前方的单个静态物体产生频率恒定为的 IF 信号。频率分辨率频率分辨率(frequency resolution)是指将两个相邻谱峰分开的能力。在实际应用中是指分辨两个不同频率信号的最小间隔。我们知道傅里叶变换能将一个时域信号转换为频域信号,且时域中的单音信号(如正弦信号)在频域中只会产生一个峰值。如下图所示。

在下图的观察窗口T内,蓝色函数完成2个周期,而红色函数完成2.5个周期。两个函数0.5 个周期的差异不足以分辨出频谱中的两个谱峰(即频率)。

将观察窗口T加倍,使个周期的差异为1个周期。则可以分辨出频谱中的两个谱峰(即频率)。

从上面的仿真结果我们可以看出,对回波信号的观察周期越长,信号处理后得到的频率分辨效果就越好。一般来说,观察时长为T的一个观察窗可以分离相隔超过1/T Hz的频率分量。距离分辨率距离分辨率是雷达在距离维度上辨别两个或更多物体的能力。当两个物体相对于雷达的距离近到某个特定值时,雷达便不能再将二者区分开,将两个物体分辨为同一个物体。如果雷达探测到多个物体,则在RX天线处会接收到多个线性调频反射波。即IF信号的频谱图将显示多个谱峰,每个谱峰所对应的频率与相关物体距雷达的距离成正比。下图显示了接收自不同物体的三个不同的RX线性调频脉冲。

其相应的频谱图如下图所示。

线性调频毫米波雷达是通过对 IF 信号频率的测量来确定目标的位置等信息。将物体区分开即为将谱峰区分开。也就是说距离分辨率转换为频率分辨率。而由上可知,观察窗口长度为的 IF 信号能将间距为的谱峰分开。故通过增加 IF 信号的长度(观察期)来可以改善距离分辨率。而信号长度的增加会使信号带宽随之变宽,因此,也可以说增加 IF 信号的带宽可以改善距离分辨率。又因为与雷达相距为的物体产生 IF 信号频率为,且只要频率差,就可以在频率上分辨出两个目标。故对相隔距离为的两目标,其 IF 频率差为,又因为观察时间是,即
式中,。由上式可得,距离分辨率 () 仅取决于线性调频信号扫过的带宽,即
采样定理采样是将一个信号(即时间或空间上的连续函数)转换成一个数值序列(即时间或空间上的离散函数)。又因为复采样定理,即采样频率大于中频带宽。故 IF 信号的最大频率取决于所需测量的最大距离:
而 IF 信号的最大频率即为 IF 信号的带宽。IF 信号为模拟信号,只有转换为数字信号(LPF ADC)才能在 DSP 中对信号进行进一步处理。而转换过程中需要对模拟信号进行采样。因此,IF 带宽受到 ADC 采样频率()的限制,即
故一个采样频率为的雷达,其最远探测距离如下图所示的两个线性调频信号,其分别具有什么优势呢?

图中,虽然两线性调频信号具有相同的距离分辨率(带宽相同),但对于相同的最远探测距离,持续时间为的线性调频信号相对于持续时间为时只需要一半的 IF 带宽(即使ADC 具有的较小);而持续时间为的线性调频信号的优先是只需要一半的测量时间。毫米波雷达信号处理框图如下图所示。

- 合成器产生一个线性调频信号;
- 线性调频信号由发射天线发射,由接收天线接收受物体反射的回波信号(该信号是发射天线发射的线性调频信号的延时);
- 中频信号由多个单音信号组成,每个单音信号的频率( )与对应物体与雷达之间的距离( )成正比;
- 中频信号需要数字化,则 ADC 必须满足中频信号的带宽 ;
- 对 ADC 数据进行 FFT,频谱中峰值的位置直接对应目标的位置,如下图所示。

这样的 FFT 被称为“距离 FFT ”。由前面叙述可知,线性调频信号的带宽与雷达距离分辨率有关,线性调频信号带宽越大,距离分辨率越好;而中频信号的带宽与最远探测距离有关,中频信号带宽越大,雷达探测距离越远。
二、中频信号的相位傅里叶变换傅立叶变换将时域信号转换为频域信息。时域中的正弦曲线在频域中会产生峰值。通常,频域中的信号是复数(即每个值都是一个具有幅度和相位的相量)。且峰值相位等于正弦波的初始相位。如下图所示。


中频信号的相位在混频器中,混频器输出信号的频率、相位均为输入信号的差值。如下时间-幅度图所示。

图中,回波信号为发射信号的延时副本,对于同一回波,其频率差是一定的。故发射信号与回波信号的相位差的即为初始相位差,即为。则两回波的相位差(即C、F之间的相位差)就等于A、D之间的相位差,即
式中,为雷达测量的“两物体”间的距离差。则距离雷达为的目标回波产生的中频信号为
式中,,。则对于一个线性调频毫米波雷达,如果雷达前方的物体改变其位置 1mm(对于 77GHz 雷达 1mm= λ/4):
- IF 信号的相位变化为
- 中频信号的频率变化为
我们可以看出,中频信号的相位对物体范围的微小变化非常敏感。一定距离的物体产生一定频率和相位的中频信号,物体的微小运动会改变 IF 信号的相位,但不会改变频率(微小的频率变化在频谱中是无法辨别的)。
三、速度估计由上述内容可知,对于单个目标,我们可以利用 IF 信号的频率来测量其距离,用 IF 信号相位变化来测量目标自身的微小变化。那么目标的速度信息该怎么测量呢?使用两个线性调频脉冲进行的速度测量为了测量速度,FMCW雷达会发射两个间隔为的线性调频信号。则与雷达相距的同一目标产生的两个 IF 信号经过距离 FFT 处理后将在同一位置出现谱峰。又由傅里叶变换的性质可得,两个位于同一位置的 IF 信号谱峰具有不同相位的峰值。如下图所示。

因为 IF 信号的相位差,故两个间隔为的线性调频信号的相位差
式中,为目标径向速度,为两发射脉冲间隔,为波长。则目标速度在两个连续的线性调频信号之间测量的相位差可用于估计物体的速度。
振动物体的测量除了速度测量之外,IF 信号的相位对微小运动非常敏感这一特性也是很多应用(例如电机振动监测、心跳监测)的基础。下图描绘了以振荡方式运动的物体的时间演变过程。这可以代表振动物体。

假设运动幅度非常小,因此物体的最大位移是波长的一小部分(例如,一毫米或更小)。如果我们在这个振荡物体的前面放置一个雷达并发射一串等距的线性调频信号,则这些线性调频信号中的每一个都会产生反射线性调频信号,而处理后的 IF 信号将产生距离 FFT 中的峰值。这些峰值的频率不会发生太大变化,但是峰值的相位将响应物体的振荡运动。下图为相位-时间图。

又,即。故相位的时间演化可用于估计振动的幅度和周期性。
最大可测量速度IF 信号的相位,故当目标远离雷达时,即;相反,当目标靠近雷达时,即。

则当相位变化到如上图所示位置时,我们如何确定目标是靠近雷达还是原理雷达,为了不产生歧异,规定雷达不模糊速度测量的相位。此时,,即
由间隔为的两个线性调频信号所能测量的最大相对速度()为因而,更大的速度需要更短的发射间隔。
同一距离上多目标速度测量如果速度不同的多个移动目标在测量时与雷达的距离相同,则双线性调频信号速度测量将方法不起作用。这些物体由于与雷达的距离相同,因而会生成IF频率完全相同的反射线性调频信号。因此,距离 FFT 会产生单个峰值,该峰值是所有这些距离相同的目标信号合并而来的。简单的相位比较技术将不起作用。在这种情况下,为了测量速度,雷达系统必须发射两个以上的线性调频脉冲。它发射一组 N 个等间隔线性调频脉冲。这组线性调频脉冲称为线性调频信号帧。下图显示了一个线性调频信号帧随时间变化的频率。

下面以两个与雷达的距离相等但速度分别为和的两个物体举例说明处理技术。距离 FFT 处理反射回来的一帧线性调频信号,从而产生一组N个位置完全相同的峰值,但每个峰值都有一个不同的相位,包含来自这两个物体的相位成分(来自各个物体的单独相位成分由下图中的红色和蓝色相量表示)。

对与距离 FFT 峰值相对应的相量序列进行 FFT 来解析这两个对象。这称为多普勒-FFT,多普勒 FFT在 N 个相量上执行,以分辨两个物体,多普勒 FFT 结果如下图所示。

和对应于各个物体连续线性调频信号之间的相位差,则目标速度为
速度分辨率由傅里叶性质可得,连续信号的频率分辨率为:
则长度为 N 的离散序列的频率分辨率为:
又因为频率差,故速度分辨率

如上图所示,雷达的速度分辨率与帧时间 () 成反比,由下式给出
欢迎关注公众号:雷达信号处理MATLAB
一起学习雷达信号处理相关知识及其仿真,一起学习、一起成长
,




