今天我们一起来复习和学习的有关锐角三角函数和解直角三角形的一些关键性概念和一些必须掌握中考必出的解题方法。三角函数的内容说难,其实很好理解,说不难往往做题不知道如何下手,这是很多同学无法学好数学的通病。如果我们想要中考取得高分,高中数学继续保持高分的实力,三角函数的内容是一定要深入了解的内容,现在学好了高中对应的知识也会更容易理解。锐角三角函数和解直角三角形的知识在中考数学中占15-25分,读完这篇文章相信你也可以轻松拿下。
首先我们要明白锐角三角函数的的定义,在初中阶段求锐角的三角函数值,都是通过构造直角三角形来完成的,即把这个角放到如图所示的直角三角形中,而到了高中三角函数值的求法是通过坐标定义法来完成的,这个时候角也扩充到了任意角。
一、锐角三角函数
定义:锐角三角函数是以锐角为自变量,以比值为函数值的函数。我们把锐角∠A的正弦、余弦、正切和余切都叫做∠A的锐角函数
图形的几何表达:

看完这几个公式很多同学也不会明白到底是表达了什么,其实正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化。简而言之的理解就是角度的大小决定于边的长度的比值,形成了一定的规律。因此一些特殊角的三角函数值也是一定要记住和掌握的。
30°、45°、60°、90°的正弦、余弦、正切、余切的值
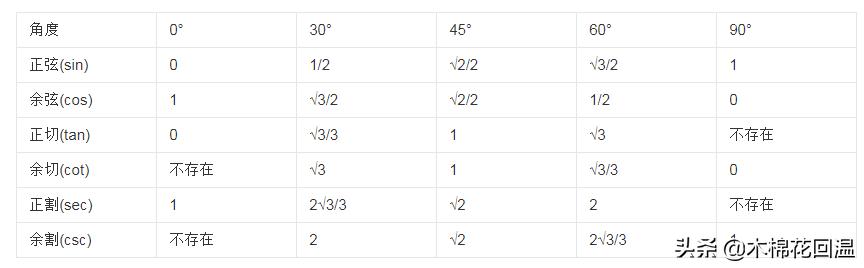
学到这里,我们就基本掌握了锐角三角函数的概念和三角函数的特殊值,下面举两个简单的例子,加深印象同时学会怎么应用。

这个题目是已知∠A的正弦值,利用赋值法和勾股定理求出三边的长度再求∠A的余弦值及∠B的正切值,这是简单求值的应用。

这是一个简单的计算题目,只要把各个特殊角度的三角函数值代入然后化简即可,这是中考数学必考的计算题之一,所以要求必须掌握。
除了正常的求值外,有一些题目会涉及到正弦、余弦、正切之间的转换,那么我们就要熟记下面四个数量关系。初中阶段可能运用的比较少,但高中时经常用到,所以可以先提前了解一下。

二、解直角三角形
定义:在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形。
在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.
设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:
①三边之间的关系:a2 b2=c2(勾股定理)
②锐角之间的关系:∠A ∠B=90°
图形的几何表达:

解题要点:
1、根据题意画出直角三角形的图形,标出已知的三角形元素,哪些角或者边已知,然后用勾股定理或者锐角三角函数的方法求出未知的元素。
2、有时候题会给出一些特殊角度的正弦值或者余弦值,例如37°等,就需要利用这个角构造直角三角形求出未知的边。
解直角三角形其实就是利用锐角三角函数的角边关系,对于实际生活问题的解决,所以通常题目很长,但是关键的已知条件就是长度和角度,只要构建好直角三角形就能够轻易解题。下面同样两个简单的例子带你轻松掌握。
经典实例:

上面是两道非常简单但是又很典型的例子,第一题已知两个角度和一条边,利用构建直角三角形ACD和CDB ,再利用已知角度的正弦余弦值可求出另外两条边的长度。第二题则是更简单的已知∠B的正切和∠DAC的余弦关系,可求出对应边的关系。
看完以上内容相信大家对于中考必考内容锐角三角函数的相关知识有一定的认识和了解,在后面的练习和考试只要谨记我说的解题步骤和思路,你也可以轻松算出答案,拿分是必然的事情。
如果大家有数学上的问题和想了解哪方面的数学知识,欢迎大家关注和私信我,谢谢。
,




