人教版数学六年级上册数与形六年级上册数学数与形

《数与形》教学设计

教学内容：人教版小学数学六年级上册107页例1及相关练习。

教学目标：

使学生通过自主探究发现图形中隐藏着的数的规律，并会应用所发现的规律；使学生会利用图形来解决一些有关数的问题。
让学生经历观察、猜想、验证、思考、归纳、合作等活动，进一步积累数形结合数学活动经验，培养学生数形结合的数学思想意识。
体验数形结合的数学思想方法价值，激发学生用数形结合思想方法解决问题的兴趣，感受数学的魅力。体会和掌握数形结合、归纳推理等基本的数学思想。

教学重点：借助“形”感受与“数”之间的关系，引导学生探索、发现规律，培养学生用“数形结合”的思想解决问题。

教学难点：在探究过程中积累基本的活动经验，感悟数形结合、归纳推理的数学思想。

教学准备：课件，磁力板，不同颜色的小正方形磁力扣。

教学过程：

一、导入：

师：今天我们来研究《数与形》看到“数”你想到了什么？数是无穷的；看到“形”你想到了什么？形也是千变万化的，看到数与形，你又想到了什么？接下来就让我们一起打开数与形的大门。

二、探究新知:

（一）以形助数

1.构造直观。

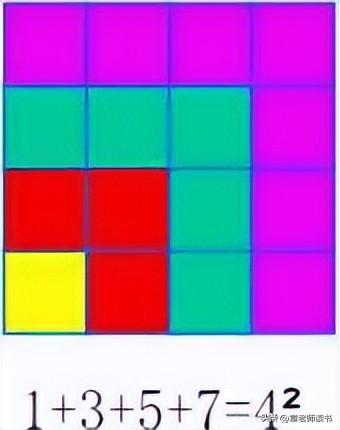
师：你看到了什么？（一个正方形）说的很对，这里面既有数又有形，我把它记录下来。（板书贴1写数字1）,这太简单了，继续看，谁能告诉我现在一共有几个正方形？（说3个是凭直觉，出现了 3个，我问的是一共几个？）快列个小算式告诉我？ 1 3=4 （边读边写）。不错！再仔细观察，下面一共几个正方形？快用个小算式表示，说原始算式吧！ 1 3 5二9,还能挑战吗？下面一共有多少个正方形？ 16个。

师：现在我不出现小正方形了，你能猜到我下一个算式会是什么吗？再下一个呢？写的完吗？写不完（加重语气点点）天呢，你们是怎么知道这些算式的？看我教案了？（他们是连续的奇数）哦，我们看这些加数是有规律的，他们都是从1开始连续的奇数（不同颜色的笔板书：从 1开始的连续奇数）。这有什么难的，这是我们之前的学习的找规律。关键的是我们看它右边的结果有什么共同特征？ 1的平方，2的平方、、、、这样的数我们叫做平方数。平方数说得完吗？还有吗？还有多少？那还写吗？你能说出一个式子来代表所有的平方数吗？（预设：a2）o

师：我们一直说这节课要研究数与形，怎么到目前为止我们都在说数呢？你看到护你想到了什么形？为什么呢？ S二护正方形的面积公式。由此我们看到这些数就想到了正方形，真不错，会联想！那你能在正方形里你能找到吕吗？（正方形涂阴影）屮也就是表示边长是a的正方形的面积。指生说一说护表示什么？谁能用刚才的句式表示表示P什么含义？ 2三呢？（边长是2的正方形的面积是2三）。

大家看，数能变成形，形也能变成数。我们看到的22在你们脑海里什么形？（正方形）边长是几？数与形的关系多么密切啊！你能在你的磁力板上表示出这个边长为2的正方形吗？（指生在黑板上粘贴）看到这个正方形你想到哪个式子？也就是1 3=4 （板书），在这个图形中“1” 在哪？ “3”在哪？这个式子就可用边长为2的正方形来表示。它的面积是26

师：那同学们，我们要探究从1开始连续奇数相加的和（板书相加的和），有什么规律？我们可以借助什么来研究？（正方形）复杂的问题先从简单的开始，接下来我们以小组为单位进行探究，请看要求。

生4人一小组进行探究活动。（大约8分钟）

师：我发现每个小组活动都非常积极，而且都很有自己的想法。哪个小组愿意上来给同学们展示一下你们的发现？

汇报展示：（要求按照步骤，先汇报摆法，再汇报发现的规律）

组1：我们小组首先用1个黄色小正方形加上3个红色小正方形拼成了一个大正方形。（算式：1 3二2?）

组2：我们先拼出和他们一样的图形，紧接着在它的基础上加了 5 个绿色小正方形拼成了一个更大正方形。（算式1 3 5二32）（你给大家说一说加法算式在哪里？你除了用加法得到9还用什么得到9? 32, 3在哪里？）

你这么快想到16,你用的什么算式？ 4=你想到了什么？边长为4 的正方形。核心问题：正方形的边长和什么有关系？（加数的个数）看到这个图你想到了加几？

你发现了什么规律？

其他组有要补充的吗？你们还有其他的发现吗？（补充发现）

2.补充完善规律。

深度思考：师：所有的数相加都有这样的规律吗？

生汇报：必须是连续的奇数相加。