找次品问题之次品特点未知的特例2——8找1“换组法”
2018年8月10日星期五
本文以《找次品问题之次品特点未知的特例1——5找1“破组法”》为基础,有了上文的铺垫,本文行文得以简洁,让我们专注于特例本身。

下面给出特例2:
8找1,即在8个产品中找出唯一的次品,并说明其特点。
首先,给8个产品编号为:①②③④⑤⑥⑦⑧。
其次,对8个产品进行分组。
8(3,3,2)
对应为:(①②③,④⑤⑥,⑦⑧)
分组依然遵循尽量“均分为三”的最优策略。
第三,开始称重。
第(一)步:
(①②③)←→(④⑤⑥)
出现两种结果:1或0
第(二)步:
分情况进行讨论。
1:
即次品在①②③④⑤⑥中,①②③与④⑤⑥或轻或重被标记一次;⑦⑧是合格品。
(①⑤⑥)←→(④⑦⑧)
出现两种结果:1或0
本步体现“换组”特点,请注意观察:用合格品⑦⑧换掉右盘⑤⑥,用右盘⑤⑥换掉左盘②③。新进入的是⑦⑧,出去的是②③。这样做的实质是:一种新的、巧妙的“均分为三”的分组方法。由于次品在①②③④⑤⑥中,正常情况我们要对这个“保留组”进行分组:6(2,2,2),但换组法巧妙之处在于:分为②③一组、⑤⑥一组、①④一组;②③在盘外,⑤⑥由右盘转为左盘,①④仍居左右两盘且不改变原来状态。像①④这样的“分居两盘组”,在“换组法”的操作下,数量为2的倍数:2、4、6、8、……这个特点对“换组法”的通用性或更大n值(比如大于12时)的优越性将带来限制,此处作为铺垫。
(重要程度★★★★)
0:
次品在⑦⑧中,①②③④⑤⑥均为合格品。任选一合格品①与⑦(或⑧)对比称重:
(①)←→(⑦)
出现两种结果:1或0
第(三)步:
由于树形结构“几何级递增”的特点,本步需讨论4种情况。
1-1:
在连续两次出现“不平衡”状态时,我们要进一步地区分:1s(状态一样)、1c(状态改变)。故而第(三)步总讨论情况数变为:4+1=5(种)。请注意这种结构的变化,您可以边读边拿起纸和笔,尝试画出“树形图”,辅助您的理解。事实上,一个“树形结构”哪怕每次分支为2,4层后也将扩展为:2^(4-1)=8种情况,如下图:
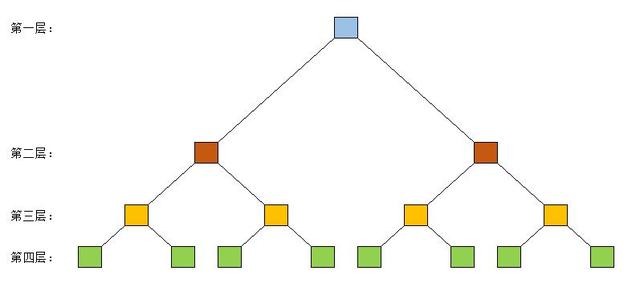
树形二分图
更别说5层、6层……更多的分支!将称重步骤用文字描述简直就是一场“灾难”!这也是我们选取n值不太大但比较典型的数值的原因,因为数学中许多规律总是可以通过较少的“有限归纳”得出的,即体现了以小见大、以有限推断无限的特点。
1-1s:
即:(①②③)←→(④⑤⑥)与(①⑤⑥)←→(④⑦⑧)的不平衡状态相同。
此时,由于⑦⑧是合格品,以下换组:⑦⑧→⑤⑥→②③未改变不平衡状态,说明⑤⑥、②③也是合格品,次品在①④中。我们可以任选①④中的一个与其他任一合格品进行第3次称重对比,便可判断出次品:
(①)←→(⑦)
出现两种结果:1或0
1-1s-1:说明①是次品,且次品特点已知;
1-1s-0:说明④是次品,且次品特点根据前两步任一步的“标记”已知。
(1▲▲▲)
1-1c:
即:(①②③)←→(④⑤⑥)与(①⑤⑥)←→(④⑦⑧)的不平衡状态相反。
此时,由于⑦⑧是合格品,以下换组:⑦⑧→⑤⑥→②③改变不平衡状态,说明次品在⑤⑥中,正是由于⑤⑥中包含次品,其由右盘换至左盘的过程使得天平的不平衡状态发生了“逆转”。⑤⑥是“同盘组”,直接对其二者进行第3次称重对比,即可找出次品:
(⑤)←→(⑥)
只会出现一种结果:1
1-1c-1:次品或⑤或⑥,且次品特点根据前两步任一步的“标记”已知,或轻或重,可以确定。
(2▲▲▲)
1-0:
即:(①②③)←→(④⑤⑥)不平衡,而(①⑤⑥)←→(④⑦⑧)平衡。
显然,次品在换出盘外的②③中。②③是“同盘组”,直接对其二者进行第3次称重对比,即可找出次品:
(②)←→(③)
只会出现一种结果:1
1-0-1:次品或②或③,且次品特点根据第一步的“标记”已知,或轻或重,可以确定。
(3▲▲▲)
0-1:
即:(①②③)←→(④⑤⑥)平衡,(①)←→(⑦)不平衡。
此时:⑦是次品,对比合格品①,特点已知。本情况下称重2次找出次品。
(4▲▲▲)
0-0:
即:(①②③)←→(④⑤⑥)平衡,(①)←→(⑦)平衡。
此时:⑧是次品,特点未知,和任一合格品对比第3次即可确定:
(①)←→(⑧)
只有一种结果:1
0-0-1:次品是⑧,特点已知。
(5▲▲▲)
此时用(▲▲▲)标记的5种情况均已讨论完备,足见:8找1次品特点未知最少3次保证可以找出。
完整“树形结构”图示如下:

“8找1次品特点未知”称重实验示意图
或许,您可以在纸上画一画,将具体的天平称重示意图添加进上面的树形图中,更加直观,有益于您的理解和思考。
对于“8找1次品特点未知”的情况,按我的“通用模型”(下文将给出),最少需称重4次,但巧妙的“换组法”进一步地优化到了3次,这与上文“公式A”的结论凑巧一致。本例如果再用上文“破组法”,则优化不出3次的结果,因为第一次称重时,盘中各有3个,不能均分破组。
“换组法”的强大之处还在于最大可将“12找1次品特点未知”的次数优化到3次,“13找1”、 “14找1”……便办不到了。进一步扩大到“29找1”时,“公式A”的解为:4 1=5次,我的“通用模型”解为4次,“换组法”也是4次。
“换组法”操作麻烦,易出错,不易理解。我现阶段的观点是:n>12以后,“换组法”相较我的“通用模型”,不再具有优势。(后文详述)
下面给出“12找1次品特点未知”的简要称重实验过程:

“12找1次品特点未知”称重实验示意图
值得注意的是:
(1)1s、1c符号只在两次均出现不平衡状态,且盘内产品数保持一致的情况下使用,也就是此时才有对比“不平衡状态是否发生改变”的必要。
(2)上面“12找1次品特点未知”的实验过程中,第二次对①②③④⑤⑥⑦⑧通过“换组”实现“均分为三”的过程为:8(3,3,2),对应为:(②③④,⑥⑦⑧,①⑤),所以“节约次数”,正是由于每小组均不超过3的缘故,使得各小组在接下来只需称重1次即可确定次品,这一点对于理解“换组法”的特点和限制尤为重要。
,




