
平行线的判定和性质的知识是初中几何的基础内容,这部分知识掌握的好坏关乎整个初中几何知识的成败,所以同学们一定要打好这一基础关,为后续的学习铺平康庄大道。
☞平行线的判定,初一常用的有六种方法:①定义法,同一平面内不相交的两条直线是平行线;②平行于同一条直线的两条直线平行;③两条直线被第三条直线所截,同位角相等,两直线平行;④两条直线被第三条直线所截,内错角相等,两直线平行;⑤两条直线被第三条直线所截,用旁内角互补,两直线平行;⑥在同一平面内,垂直于同一条直线的两条直线平行.
☞平行线的性质:两条平行线被第三条直线所截,①同位角相等;②内错角相等;③同旁内角互补.
【题目呈现】
例1.如图,在三角形ABC中,CD⊥AB,E,F,G分别在BC,AB,AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由.
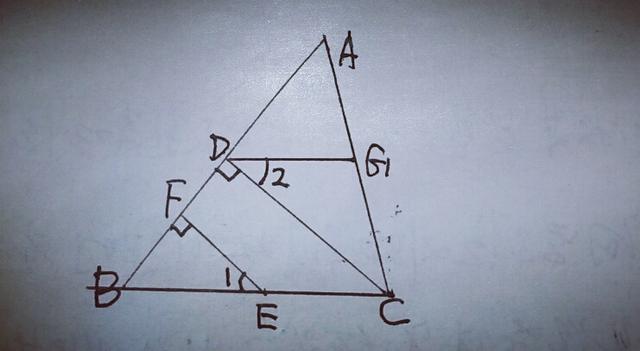
【分析】观察图形,DG应与BC平行,那么我们假定DG∥BC,看能推出的某些结论是否与已知条件相同,若相同了,则说明假定是正确的,若不相同或与已知矛盾或与某些定理矛盾,则假定是错误的.我们分析一下,若DG∥BC,则可推出,∠2=∠DCB,又∠1=∠2,则∠1=∠DCB,则EF∥DG,则∠BFE=∠BDC,而已知中CD⊥AB,EF⊥AB,则EF∥DG,则∠BFE=∠BDC,所以假定是正确的.另外也可以估计DG∥BC,我们看从条件是否能证出来,那么我们就大脑中搜索证明两线平行的六种方法,再结合图形看如何找具体的关系,应该试着这样考虑:①可证∠AGD=∠ACB(利用同位角相等,两直线平行推出DG∥BC).②可证∠2=∠DCB(利用内错角相等,两直线平行推出DG∥BC).③可证∠ADG=∠ABC(利用同位角相等,两直线平行推出DG∥BC).④可证∠DGC ∠GCB=180°(利用同旁内角互补,两直线平行推出DG∥BC).⑤可证∠GDB ∠DBC=180°(利用同旁内角互补,两直线平行推出DG∥BC).这5种方法脑海中闪过之后,结合条件∠1=∠2,题中有∠2出现,应用第②种方法为好,欲证∠2=∠DCB,则须证∠1=∠DCB,再看条件,CD⊥AB,EF⊥AB,则可推出EF∥DC,则可得到,∠1=∠DCB,这样问題得证.可见,有了方法之后,还看步步结合条件,步步为营,直到解决问题,这是初学者必须掌握的最基本的证明方法.分析完之后,初学者还要掌握正确的书写步骤,大多同学手懒,不写,不想写,有很多同学到了初二,初三也不会写步骤,以致明知该题如何做,考分下来之后不理想,所以我们要多写,勤写,准确写出具体步骤,初一写步骤过关之后,初二初三就轻松得多了,而且几何证明题,能证出来就能写出来.
【解题过程】
解:DG∥BC.理由知下:
∵CD⊥AB,EF⊥AB(已知),
∴CD∥EF(在同一平面内,垂直于同一直线的两直线平行),
∴∠1=∠DCB(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠2=∠DCB(等量代换),
∴DG∥BC(内错角相等,两直线平行).
【对应练习】
☞1.如图,已知AD⊥BC,FG⊥BC,垂足分別为D,G,且∠ADE=∠CFG,求证DE∥AC.

2.如图,已知∠ABC=180°一∠A,BD⊥CD于D,EF⊥CD于F.
(1)求证:AD∥BC;
(2)若∠1=36°,求∠2的度数.

例2.如图,已知∠1 ∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系.

【分析】估计∠AED=∠C,看通过条件能否推出,欲证∠AED=∠C,须证∠ADE=∠B,(有的同学问,你怎么就知道证∠ADE=∠B呢?其实也可以从其他方面想,因为条件中有∠B=∠3,出现了∠B,所以我先想到利用∠B,也就想到要证∠B=∠ADE,况且∠ADE与∠3是内错角,而条件中也出现了∠3,若能证明了∠ADE=∠3,则就能证明了∠B=∠ADE,这样又须证明AB∥EF,结合条件∠2的出现,又须证明∠2=∠4,而∠1 ∠2=180°,又∠1 ∠4=180°,∴∠2=∠4,∴问题圆满得解.
【解答过程】
解:∵∠1 ∠4=180°(邻补角定义),
又∵∠1 ∠4=180°(已知),
∴∠2=∠4(同角的补角相等),
∴EF∥AB(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等).
又∵∠B=∠3(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
例3.如图,已知AB∥DC,∠BAD=∠DCB,说明AD∥BC.

【分析】此题不难,可有的同学不知道要证AD∥BC,需要找哪两个角的关系,若要用"内错角相等,两直线平行“,应该用∠1=∠2,而不能用∠3=∠4,若要用同旁内角互补,两直线平行,应该用∠BAD ∠ABD=180°,或∠ADC ∠DCB=180°,而不能用∠BAD ∠ADC=180°,或∠ABC ∠DCB=180°,换句话说,有的同学不明白,内错角相等推出哪两条线平行;同旁内角互补推出哪两条线平行,或者不明白,两条直线平行,推出哪两个角相等,哪两个角互补.就拿本题来说,AB∥DC,∠3的边AC与∠4的边CA重合,AC是截线∠3的另一边AB与∠4的另一边CD,是被截线,两条被截线平行,只能推出∠3与∠4这一对内错角相等,而推不出∠1=∠2,∠1的边AC虽然与∠2的边CA重合为AC,但∠1的另一边是AD,∠2的另一边是BC,它们两边既不是AB又不是CD,∴AB∥CD只能推出∠3=∠4,可见,两线平行,只能推出与两线有关的角的关系,同样通过两角的关系也只能推出与角有关的线平行,而且是被截线平行,明白了这层关系本题也就解答了.
【解答过程】
解:∵AB∥DC(已知),
∴∠3=∠4(两直线平行,内错角相等).
又∠1=∠BAD一∠3,∠2=∠DCB一∠4,且∠BAD=∠DCB(已知),
∴∠1=∠2(等式的性质),
∴AD∥BC(内错角相等,两直线平行).
当然本题也可用同旁内角互补证得.
例4.如图,DE⊥AC,∠AGF=∠ABC,∠1 ∠2=180°,试判断BF和AC的关系,并说明理由.

【分析】BF与AC的关系应是互相垂直,题中已有DE⊥AC,则只要推出BF∥DE即可,从图看,应证∠2 ∠3=180°,再结合∠1十∠2=180°,应证∠1=∠3,须证FG∥BC,而又有条件∠AGF=∠ABC,则可得FG∥BC,得证.
【解答过程】
解:BF和AC的关系是互相垂直,理由如下:
∵∠AGF=∠ABC(已知),
∴GF∥BC(同位角相等,两直线平行),
∴∠1=∠3(两直线平行,内错角相等).
∵∠1 ∠2=180°(已知),
∴∠3 ∠2=180°,
∴BF∥DE(同旁内角互补,两直线平行),
∴∠BFC=∠DEC(两直线平行,同位角相等),
∵DE⊥AC(已知),
∴∠DEC=90°(垂直定义),
∴∠BFC=90°,
∴BF⊥AC(垂直定义).
例5.如图,已知∠1=∠2,∠3=∠4,∠5=∠6,请问:AD和BC平行吗?说明理由.

【分析】AD可能与BC平行,观察条件,∠1=∠2,∠3=∠4,看不出什么,而∠5=∠6,可推出ED∥AB,抓住这一条件就找到了突破口,一直推下去可得到解答,ED∥AB,可得∠3=∠7,而∠3=∠4,∴∠4=∠7,可得AE∥BD,则可得∠2=∠8,而∠2=∠1,则∠1=∠8,∴AD∥BC,得证.
【解答过程】
解:AD与BC平行,理由如下:
∵∠5=∠6(已知),
∴ED∥AB(内错角相等,两直线平行),
∴∠3=∠7(两直线平行,内错角相等).
∵∠3=∠4(已知),
∴∠4=∠7(等量代换),
∴AE∥BD(同位角相等,两直线平行),
∴∠2=∠8(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠8(等量代换),
∴AD∥BC(内错角相等,两直线平行).
也可以这样证,简单写一下,在△AED中,∠2=180°一∠4一∠6,在△ABD中,∠8=180°一∠3一∠5,而∠3=∠4,∠5=∠6,∴∠2=∠8,又∠1=∠2,∴∠1=∠8,∴AD∥BC.
【总结】相交线与平行线这部分知识一般不难,注意平行线的判定与性质的相互运用,通过平行关系,立即推角的关系,通过角的关系联系条件,得到下一组角的关系,再得到下一组线平行,这样相互推证,最终获解,注意书写规范,图果关系明确,推证合理.
感谢大家的关注、转发、点赞、交流!
,




