15 爱因斯坦再次出场
爱因斯坦此前的工作表明,黑体辐射是辐射场的涨落,黑体辐射分布函数 1/(ehν/kT-1) 中的 “-1” 在辐射—双能级分子模型中明确来自受激辐射机制。爱因斯坦一直对热力学、统计力学感兴趣,我甚至觉得爱因斯坦并未区分什么物理的领域,他只是研究物理而已。前面说过,阅读爱因斯坦论文时每一个字都不可以漏过。我不敢说其中的每一个字都包含物理,但我感觉其中的每一个字都对我理解物理有帮助。
玻色的黑体辐射推导勾起了爱因斯坦的兴趣,估计他在给玻色翻译论文的过程中就完成了自己的推导。爱因斯坦果断中断了当时占据他脑海的统一场论研究,转过来谈统计问题,而这本是他的拿手好戏。结果是,爱因斯坦迅速两篇论文出手,其中第一篇分两部分发表:
(1) Albert Einstein, Quantentheorie des einatomigen idealen Gases (单原子理想气体的量子理论),Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, 261-267 (1924).
(2)Albert Einstein, Quantentheorie des einatomigen idealen Gases, zweite Abhandlung (单原子理想气体的量子理论之二),Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, 3-14 (1925).
(3)Albert Einstein, Zur Quantentheorie des idealen Gases (理想气体的量子理论),Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, 1825 (1925).
爱因斯坦这两篇文章之后的统计力学有了量子统计的面貌。
这两篇论文,因为题目相似,其1925年的“理想气体的量子理论”一文连wikipedia的Bose—Einstein statistics和Bose—Einstein condensate条目都是忽略的。爱因斯坦的第一篇(分为两部分的)文章,表述中连字母使用都有点儿忙乱,不是很好懂。笔者愚鲁,一时不能拿捏准确。
玻色的推导方式,提供了得到单原子理想气体量子理论的途径。系统组成单元(原子)的相空间可分成h3大小的相空间单胞,许多个基本单元组成的体系的热力学由系统基本单元在这些相空间单胞里的分布所决定。宏观状态的概率由实现该宏观状态的微观状态数表征,这样的体系满足玻尔兹曼定律。体积为V 的物理空间里色散关系为

的粒子,其能量E之下部分的相空间体积为


,在能量范围ΔE内的相空间单胞数为

。假设在E→E ΔE内有粒子数Δn,这些相空间单胞中有r-个粒子的数目为prΔs (r=0,1,2,3,…). 显然,属于s-单胞的概率pr当然也是s的函数,须加个s-标记。这样,可得

,分布数为

。根据Sterling公式

和
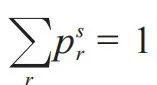
,得

{原文如此}。对于整个体系,熵表达式为

。接下来是类似玻色的推导。不得不说,这篇文章,因为其中变量s一会儿用作指标,一会儿是当作实实在在的整数,算是爱因斯坦的文章中表达最糟糕的一篇,笔者就不尝试改写了。反正,按照玻色的相空间体积量子化的思想,最后推导出了(每摩尔)理想气体熵的表达式为

,统计物理的教科书大体会直接照抄这个结果。{有机会我要找找看有没有表达更清楚的}但是,有个问题,对于一个由 n1 n2 个性质几乎一样的两种分子组成的体系,总的熵按说应该等于 N=n1 n2 个分子所组成的体系的熵,基于上述推导的结果好像不对啊。用爱因斯坦的顽皮话说,Dies erscheint aber so gut wie unmöglich (想美事儿呢) 。
在这篇文章的第二部分,爱因斯坦注意到普朗克谱分布与维恩分布之间的偏差,同他得到的理想气体统计规律与经典玻尔兹曼理论之间的偏差 {退化,见下} 有些类似。{爱因斯坦这里用到的是Entartung这个词,这个词后来在统计物理里一概汉译成简并,故有些句子不好懂。Entartung这个词儿按照退化理解比较好,比如从普朗克分布回到维恩分布就可以理解为退化,这也是Entar‐tung,degeneration,在数学中的本意。简并在物理里有相同能量的能级,矩阵有相同的几个本征值的语境下才是没有歧义的} 爱因斯坦觉得作为量子气体的辐射和分子气体之间的类比应该是全面的。由上篇的结论,对于给定温度T和V,最大粒子数为

{这里求和是从1开始的吗?看不清。先存疑},那么体系如果有更多粒子呢?多出的粒子去占据动能为零的状态,类似将蒸汽等温压缩到饱和体积以下。凝聚部分和饱和部分的普朗克函数

都为0。这是一种没有吸引前提下的凝聚。此篇论文首次提出了后来被称为玻色—爱因斯坦凝聚的凝聚概念。据说爱因斯坦发表这个结果时,受到了艾伦菲斯特的批评,具体内容待考。这个要到艾伦菲斯特的著作中去找。
在1925年的另一篇文章中,爱因斯坦重新对玻色统计的问题进行了梳理。爱因斯坦觉得光量子,先不论那个偏振的事情,和理想气体的差别就是量子质量为零的事儿。因为大家对此前的推导不认账 (指另一位统计物理大拿艾伦菲斯特有异议),我只好再寻找不包含任意假设的考量。给定体积V内质量为m的分子,设温度为T,求其分布函数,

,L=

,即假设动量以动能 L 的形式出现在分布函数中。我们不假设气压是由按照力学规律的互相碰撞决定的,那样又会得到经典状态方程。考察S = k lnW中的W,根据玻尔兹曼的量子论,那应该是个整数。熵不包含任意可加常量 (additive Konstant),而应是一个确定的数!这个普朗克表达S = k lnW 就能斯特 (Walther Nernst,1864—1941) 定理看来是必须的。绝对零度下热激发无序都停止了,系统状态只有一种可能,W=1,故有S=0。这让我们确信,熵不可为负。{这是到目前为止我在爱因斯坦论文里发现的第一句让我瞧不上的话。熵是广延物理量、标量,当然不可为负。爱因斯坦还对着经典气体理论中的RlnV这一项在那里讨论一番,说什么V变得足够小这项熵值会是负的,故经典状态方程应该抛弃,云云。奇怪,这可不是爱因斯坦的水平啊。lnV这种表述是完全错误的。物理函数的宗量 (argument) 必须是无量纲的,小学生都知道。爱因斯坦在论文里可是善用量纲考量(Dimensionalbetrachtung)的啊}爱因斯坦紧接着就认定分布函数应该写成

的形式,即分布函数是两个独立变量的函数,{看看,变量都弄成无量纲的组合了。但我很奇怪,为什么不选择更合理的
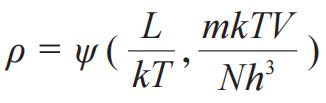
的形式}这个分布函数应该满足要求条件

,而


。可循着如下两条线索来研究分布函数的性质,目的是表明这个两变量的函数ψ是个单变量函数:(1)绝热压缩过程不改变体系的熵;(2)也存在外加保守力下的静态对应这个分布函数。考察

,分布会怎么随压缩尺度

改变呢?根据弹性碰撞理论,某方向上的动量绝对值改变为

,{这个我是真不理解了。气体体系一个方向上压缩了,为啥对应的动量改变是这样的?}动能改变为


,也即可得到

,Δ(VdΦ)=0。绝热体积变化过程不引起

的变化,即

,故Δρ=0。结论是,绝热体积变化过程不引起分布函数的变化。
针对

表达其状态分布的气体,假设其熵对于动能,如同辐射情形对于频率,是加和性的(additiv)。设动量体积微元dΦ内粒子贡献的熵为
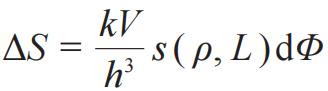
,{熵为什么要正比于元胞 (Zelle) 数VdΦ/h3啊?是基于ln(1 x)~x所做的近似?}其中s(ρ, L)是个依赖于动能L和分布函数ρ的(熵)函数。考察绝热压缩过程熵不变,{是熵微分不变} ΔdS=0,

,但Δρ=0,所以有∂s/∂L=0。结论是这个熵函数就独独是分布函数的函数,

,此必须在
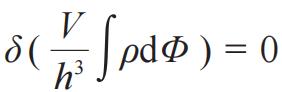
和

下取极值,变分条件是

。但因为s=s(ρ),所以ρ=ψ(AL B),函数ψ形式待定。考察等密加热 (isopyknische Erwärmung) 过程,DE=TdS,D是这个过程的微分符号,爱因斯坦又是一通操作,得到了

,k应该是个意义待明确的常数。进一步地,考察保守外场下状态方程不变,得到

,其中

,χ是一个待定函数。根据麦克斯韦推导麦克斯韦分布律的过程,这个

中的ψ函数是ψ(x)=e-x。爱因斯坦统计对应的是ψ(x)

。爱因斯坦这篇文章强调两点:

,其中

,是理想气体的一般形式,绝热压缩过程和保守外场不影响状态方程。关于气体统计,有个特征量

,那是个纯数目。
爱因斯坦1926年和1927年的两篇与光子有关的文章也值得关注,分别是:
(1) Albert Einstein, Vorschlag zu einem die Natur des elementaren Strahlungs-emissions-prozesses betreffenden Experiment (关于与基本辐射发射过程之本质有关的实验的建议),Naturwissenschaften 14,300-301 (1926).
(2) Albert Einstein. Theoretisches und Experimentelles zur Frage der Lichtentstehung (光产生问题的理论与实验考量), Zeitschrift für angewandte Chemie 40,546 (1927).
行文至此,笔者以为就黑体辐射而言,爱因斯坦的研究是最深刻的,也是收获最大的。爱因斯坦的黑体辐射研究收获总结如下:
(1) 解释了光电效应、斯塔克效应等;
(2) 建立了固体量子论;
(3) 发展了涨落理论,认识到光的波粒二象性;
(4) 得出delta函数和用Dirac-comb表示的态密度分布;
(5) 得出e与h的内在关系;
(6) 提出受激辐射概念;
(7) 导出玻色—爱因斯坦统计;
(8) 提出玻色—爱因斯坦凝聚。
有趣的是,基于受激辐射概念人类实现了激光,多年后激光冷却技术让玻色—爱因斯坦凝聚成为可能,而它们都是推导黑体辐射公式之努力的结果。黑体辐射是第一个相对论统计研究,在狭义相对论出现之前,后来又引出了量子力学。黑体辐射之意义,由此观之,怎么强调都不为过。
16 玻色—爱因斯坦统计与费米—狄拉克统计
玻色和爱因斯坦的1924—1925年间的工作算是建立起了玻色—爱因斯坦凝聚的理论。推导玻色—爱因斯坦统计的微正则系综 (microcanonical ensemble)16)模型考虑的情景是gi个能量为εi的能级上放ni个粒子,这个状态的多样性为

,{多样性,英文的multiplicity,是那个德语的Komplexionszahl(复合体数目)吗?} 在∑ni = N,∑εi ni = E的约束下求极大,即得玻色—爱因斯坦统计。
巨正则系综(Grand Canonical ensemble). 配分函数
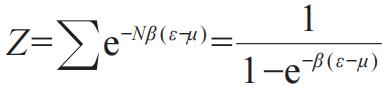
,求得平均能级上的粒子数为

。{我还是那个疑问,凭什么配分函数是这样的?没告诉学习者这个化学势,μ,是哪儿来的。}
正则系综(Canonical ensemble). 这个推导很长,且只在大粒子数的渐近极限下得到玻色—爱因斯坦分布。假设粒子有用 i 标记的简并度为gi、能量为εi 的能级。则ni个玻色子的分布方式
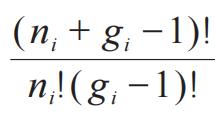
,则总的分布数

。但是,接下来又是固定粒子数和固定能量的讨论。但是,不对啊,我记得canonical ensemble的能量不是固定的。据说Darwin—Fowler method是一种非常好的推导。参考文献如下,容慢慢研读了再增补:
(1) C. G. Darwin, R. H. Fowler, On the partition of energy, Philosophical Magazine Series 6, 44, 450-479 (1922).
(2) C. G. Darwin, R. H. Fowler, On the partition of energy. Part II. Statistical principles and thermodynamics, Philosophical Magazine Series 6, 44, 823-842 (1922).
(3) R. H. Fowler, Statistical Mechanics, Cambridge University Press (1952).
与玻色—爱因斯坦统计对应的还有费米—狄拉克统计。费米—狄拉克统计是1926年由意大利物理学家费米和英国物理学家狄拉克独立提出的。费米 (Enrico Fermi,1901—1954) 1926年3月提交的一篇论文,题目和爱因斯坦1924年的论文几乎一模一样 [Enrico Fermi,Zur Quantelung des idealen Einatomigen Gases (理想单原子气体的量子化),Zeitschriftfür Physik 36,902-912 (1926) ]。{费米的这篇论文是一篇标准的外国人写的德语论文。请注意,德语很诡异,德国人自己一般都写不好,非德国人更是很难写得像样。希腊人Κωνσταντίνος Καραθεοδωρή (Constantin Carathéodory,1873—1950) 的热力学第二定律的公理化表达那篇文章是外国人写的真德语,格外稀罕}费米指出,低温下分子运动量子化,其行为同经典理论有偏差,{前面的退化。费米用了Entartung,Entartungserscheinung,Entartungstheorie等词,对应德语动词abweichen,偏差} 解释这些偏差的理论会采用这样或那样的假设,而作者发现只需要假设系统里不可以存在量子数相同的两个等值单元(nie zwei gleichwertige Elemente vorkommen können,deren Quantenzahlen vollständig übereinstimmen)即可。{是不是从数学得来的考虑呢?}
关于理想气体的行为,由分子间完全独立而得到的分子运动的量子化还是不够的(当体积足够大时,由边界条件约束而来的能量值的量子化问题实际上消失了)。为此可参考泡利1924年引入的不相容原理[Wolfgang Pauli, Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren(原子中电子群体的闭合同谱线复杂结构之间的关系),Zeitschrift für Physik 31(1),765-783 (1925) ]。{闭合,Abschuss,指电子壳层的闭合问题}作者的技巧是将分子置于一个力场下获得周期化的运动,{由此赋予量子数?}但知道统计与外加力场无关。费米施加力场使得分子成了一个振子,频率为ν,相应的势能为u=2π2ν2mr2。振子的量子数有三个s1,s2,s3。泡利原理此处可理解为,“对应一组量子数(s1,s2,s3)只有一个分子。”这样,对应能量εs=s⋅hν=(s1 s2 s3)hν,最多有Qs=(s 1)(s 2)/2个分子。这样,在绝对零度时,此中气体的分子从能量上构成一个壳层结构。这样,设能量为s⋅hν的粒子数为Ns,平衡态对应
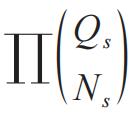
最大值(这个记号就是组合数),条件为

,

。有总分子数
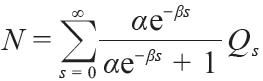
和总能量单元数

。这样的分布,后来狄拉克把它叫做费米分布 [P. A. M. Dirac, The principles of quantum mechanics, 1st edition, Oxford University Press(1930)]。
顺带说一句,
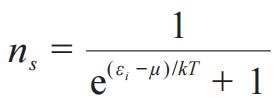
这样的函数被称为logistic function或者sigmoid function。
狄拉克在量子力学语境里讨论理想气体 [P. A. M. Dirac, On the theory of quantum mechanics, Proc. Roy.Soc. London A 112,661-677 (1926) ]。在1926年8月提交的这篇文章里,他就用到了Ein‐stein—Bose Statistics一词。狄拉克统计从狄拉克一方一开始是从多电子体系波函数开始的。{黑体辐射带来了普朗克分布和光辐射能量量子化。研究原子的辐射问题,谱线位置和强度,有了量子力学。玻色关于黑体辐射的工作经过爱因斯坦到理想气体的推广有了玻色—爱因斯坦统计。而狄拉克得到费米—狄拉克统计来自对多电子体系的考虑,即多粒子体系波函数的对称性问题。为了让系统的运动积分是矩阵,满足矩阵的乘法,那多粒子体系的波函数要么是对称的,要么是deter‐minantalform (保证反对称性)。量子力学,从开始就是统计的。不要把统计和量子力学分开。量子统计出现在量子力学之前,至少是在薛定谔1926年的波动力学之前。愚以为,量子统计是个不恰当的概念,统计从来就是基于可数性、分立性,用的是整数。}
现在来找寻本征函数反对易体系的气体之状态方程,也就是一个分子只联系一个波。把波分成一定的集合 (即ensemble),每个集合里的波只联系具有相同能量的分子。设As是某集合里的波的数目,{在谈论波函数呃。这里The number of wave真是波的数目}而εs是相应的每个分子的能量,则Ns个分子同这个集合里的波相联系的分布数(相应的反对称波函数的数目)为

。{就是m个球放到n个盒子里,每个盒子里面最多只有一个,多样性,multiplicity,Komplexionszahl就是那组合数

}对熵关于粒子数的变分求极值,
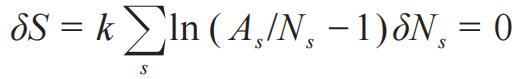
,约束条件为

,故有统计

。{从表达式看,Ns象是只能等于0,1的样子吗?这样也能用组合数学?}因
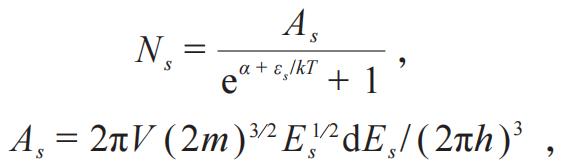
有关系式

和
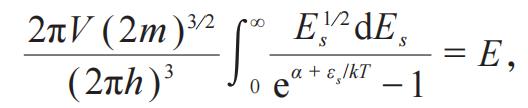
消去参数α,使用关系式

(此关系不依赖于统计),即可得到系统的状态方程。这个理论中不会出现玻色—爱因斯坦凝聚那样的饱和情形。顺带说一句,那个自旋1/2的事儿,这篇文章里可没提。
费米—狄拉克统计可以从 grand canonical ensemble,canonical ensemble,and microcanoncal ensemble 推导。
微正则系综 (Microcanonical ensemble). 用拉格朗日乘子法,分析系统的多重性。设系统有i标记的能级,能量为εi,简并度为gi,{即有gi个子能级。这个量的引入容易区分 0 和 1 ,见下}按照泡利不相容原理最多只有一个粒子可以占据这样的子能级。设能量为εi的粒子有ni个,占据方式有

,在约束

和
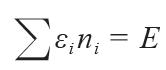
求最大。令


的变分为0,得

。
正则系综 (Canonical ensemble). 粒子数固定的一个多粒子体系,对应某个粒子数分布ni,系统能量为∑εi ni = ER,但是,系统处在这样的总能量为ER的概率为

,可表示单粒子状态的占据问题,
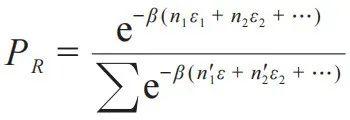
,故有某个能级的平均占据数
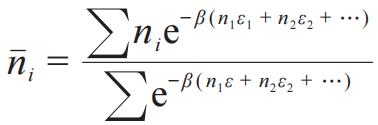
。约束条件为

,
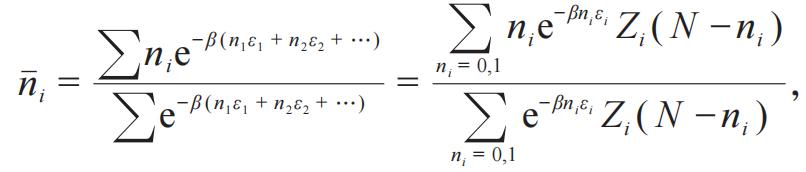
其中

。这样,则有

,记
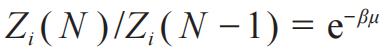
,{凑的吧?由此能计算化学势μ?}得

。
巨正则系综 (Grand canonical ensemble). 由于粒子间没有相互作用,每一个单粒子能级都是一个单独的巨正则系综,对应每一个单粒子能级系统都只有两个能量态,E=0,E=ε,故配分函数为Z=1 e-β(ε-μ),故单粒子态上的平均占据数为

。{你等等,这个μ哪儿来的?这么直接往上堆不合适吧?}
如今的文献提起费米—狄拉克统计,会谓之为量子统计,言明是遵循泡利不相容原理的粒子的统计。这个考虑是用单粒子能量状态来描述几乎没相互作用的多粒子态,但没有两个粒子处于相同的那种多体状态中。这个费米子无相互作用的统计前提让我非常十分很困惑。如何将电子纳入无相互作用体系的图像的呢?或者是在将相互作用纳入了背景以后的问题中才使用的统计?

图26 谈论约当投稿被耽误一事的文献截图[取自E. Schücking,Physics Today ]
据信,费米—狄拉克统计是1925年由约当 (Pascua lJordan,1902—1980)先推导出来的,并且他称之为泡利统计[Jürgen Ehlers,Engelbert Schücking,Jordan, Pauli,Politics,Brecht,and a Variable Gravitational Constant,Physics Today 52(10), 26-31 (1999); Jürgen Ehlers, Engelbert Schücking,Aber Jordan war der Erste (约当才是第一个),Physik Journal 1(11),71-74 (2002)]。约当把论文投给了Zeitschriftfür Physik,而主编玻恩老师把稿件往抽屉里一塞去了美国,半年后回来再拿出这篇论文,费米的论文已经发表了(图26)。在约当的《量子基础上的统计力学》(Statistische Mechanik auf quantentheoretischer Grundlage,Vieweg (1933))一书里,约当提到这个统计,但不提任何人的名字,其中悲愤,估计别人是无法体会的。此外,波动力学最关键的关系式 p→iℏ∂ 也是约当于1925年及时提出来的。没有这个关系式,哪有1926年薛定谔的方程用于氢原子问题,即把一个形式方程转化成一个具体的二阶微分方程?
,




