透视投影将可视空间定义在一个视锥体内,视锥体内的场景才是可见的,将视锥体之外的物体剔除的过程就是裁剪。如果不进行裁剪,极度靠近观察点或者观察点的背面的场景会导致扭曲或不正确的绘制效果;另一方面,裁剪避免了可视空间之外的物体参与运算,可以减少大量不必要的运算资源。

整体来说,裁剪就是判断物体与六个裁剪面(近裁切面、远裁切面、左裁切面、右裁切面、上裁切面、下裁切面)的位置关系,如果物体全部在裁切面之内则保留,全部在裁切面之外则丢弃,相交的情况需要求与裁剪面的交点以保留在裁切面内的部分。解答了下面三个问题也就明白该如何执行裁剪程序了:
- 怎么样通过数学方程来表示一个平面?
- 怎么判断一个点在平面内还是平面外?
- 怎么求解物体和平面的交点?
鉴于三角形是组成3D物体的基本单元,本文以三角形为例讲解裁剪的实现原理,虽然直接按照原理介绍的方法编程实现效率不高,但是理解了实现的原理再去掌握优化裁剪算法就不是问题了,本文不涉及优化算法的介绍。
如何表示一个平面?不在同一条直线上的三个点可以确定一个平面,参见下图,a、b、c为平面中已知的三个点,normal为该平面的法向量(可以通过向量ab、ac的叉积求得),根据点积的几何意义可知平面任意点p组成的向量pa与normal的点积为0,即平面方程可以通过如下的形式表示:
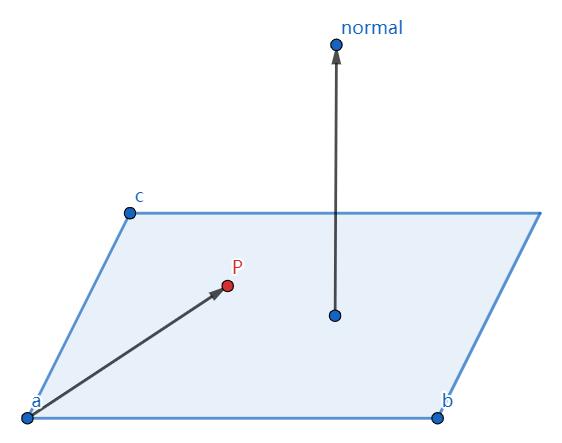

要确定一个点在平面内还是平面外首先要确定平面内、外的条件是什么,这里约定法向量normal指向(法向量方向以右手定则确定)的一侧为平面内,反方向则为平面外。确定了平面内外的准则之后,根据上面得出的平面方程可知所有在平面上的点p叉积的结果为0,那么平面内的点p组成的向量pa与normal的夹角小于90°,因此叉积大于0;类似地,平面外的点由于夹角大于90°小于270°,叉积显然小于0,参见下图。

由此可以根据点代入平面方程的正负来判断是否在平面内

三角形和平面的位置关系只需要判断三个顶点和平面的关系即可,也就是通过将顶点坐标代入上面提到的平面方程判断正负。可以汇总为四种情况:三角形全部在平面内、三角形全部在平面外、三角形一个顶点在平面内另外两个在平面外、三角形两个顶点在平面内另外一个在平面外,参见下图。

根据上面的图示可以明显得出下面的判断结果:
- 三角形三个顶点均在平面内,则保留三角形;
- 三角形三个顶点均在平面外,则丢弃三角形;
- 三角形一个顶点在内,另外两个在外,裁切后形成一个新的三角形,保留由两个交点和另外一个平面内的顶点组成的三角形;
- 三角形两个顶点在内,另外一个在外,裁切后可以组成两个三角形,保留由两个交点和另外两个平面内顶点组成的两个三角形;
这里还需要知道如何求线段和平面的交点,也就是直线和平面共点,根据直线的方程和平面的方程容易推导出交点的计算公式

首先,视锥体由六个面组成,可以通过选取视锥体上的三个顶点来确定一个面,根据三角形相似性原理可以很容易得出每个顶点的坐标。其次,要注意通过控制求法向量的叉积顺序来控制法向量全部都指向视锥体的内部。

最后,每一个三角形要依次和六个裁切面进行判断并执行裁切,需要注意的是和下一个裁切面进行判断并裁切的不是原始的三角形,而是上一次裁切后的结果(可能包含多个三角形)。
参考文献[1]. Clipping - Computer Graphics from Scratch - Gabriel Gambetta[2]. 《Essentials of Computer Graphics 5th edition》9.1.4 Clipping, Page189.
,




