作业中对同位角的理解错误剖析

人教版七年级下册《相交线与平行线》中,对三线八角的理解是基础,然后再学习平行线,通常情况下,教材中对三线八角的识别难度并不高,因此,学生在面对后续章节中较复杂的图形时,如果在前面对同位角理解不够透彻,那么,便会导致一系列识图问题。本文选择了一次作业中的一道证明题,通过面批作业过程中,学生的反应,剖析错误生成的原因,以便于在后面的教学中强化学生识图能力,同时也有针对性对学生的学习习惯提出改进要求。
题目:
已知:如图,直线AB∥CD,直线EF与AB,CD分别相交于点M,N,∠1=∠2,求证:MP∥NQ
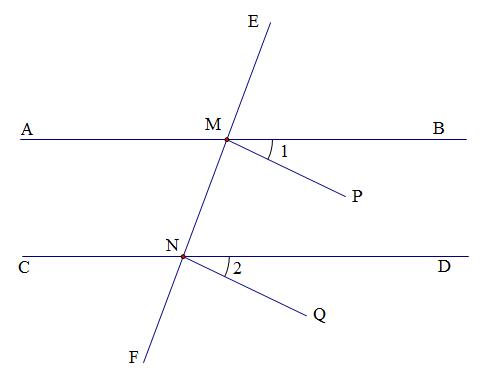
学生的错解倒也干脆,非常简单,如下:
∵∠1=∠2(已知)
∴MP∥NQ(同位角相等,两直线平行)
看完后十分无语,于是问该生:∠1和∠2是同位角吗?
答:是的,它们位置相同。
分析错误原因,显然搞错了同位角的概念,在学习同位角时,再三强调前提是两条直线被第三条直线所截,看来学生并没有真正理解截线,三线八角中的三线没能在学生脑子中留下印象。曾经在前一篇文章中提到找同位角的关键,看来在这位学生身上没有起到效果。
猜测该学生在理解同位角的概念时,还真是顾名思义,同位角,位置相同的角,而且对位置相同极为重视,甚至忽视了前提条件。再看图中的∠1和∠2,它们又是由哪两条直线被哪根直线所截形成的呢?在抛出这个问题之后,学生终于意识到了错误所在。
当只看三根直线时,才有同位角的存在,但∠1和∠2的两边已经涉及到四条线了,因此它们根本不是同位角。
继续引导,既然∠1和∠2不是同位角,那么想证明MP∥NQ,到底该证什么角呢?图中有没有它们之间的同位角?
按三线八角的识别方法,首先确定MP和NQ这两条直线,然后找截线,很容易,只能是EF,用红色笔描出它们,学生便能找到了,如下图:

图中∠3和∠4才是MP与NQ被EF所截形成的同位角,由已知条件中AB∥CD,可得到∠BMN=∠DNF,从它们中分别减掉∠1和∠2,则剩下的∠3=∠4,于是便可证明MP∥NQ,然后学生书写改错,但我还是高兴得太早了,她的书写过程如下:
∵AB∥CD(已知)
∴∠BMN=∠NDF(两直线平行,同位角相等)
∵∠1=∠2(已知)
∴∠BMN-∠1=∠NDF-∠2(等式性质)
∴∠3=∠4(同位角相等)
∴MP∥NQ(两直线平行)
我十分诧异地问她,∠3=∠4后面的理由为什么只写同位角相等?这不是一整句话吗?她回答,是啊,还有半句在下面写了。
顿时我意识到,该生的问题绝不仅仅是识图,而是对判定定理的理解上。在写下同位角相等的同时,我相信那一刻,她脑子里想到的是“∠3和∠4是同位角,所以它们相等”,而在写下一步理由的时候,脑子里想到的是“同位角上面已经写了相等了,所以理由就是两直线平行”,完全是一团浆糊。
几何证明过程中,每一步后面书写的理由,是指∠3=∠4的理由,即为什么∠3=∠4,如果回答因为它们是同位角,所以相等,那么就相当于把定理前半句作为一个判断而不是一句条件,这就是理解错误。
耐心解释,∠3=∠4成立,是因为上一步,利用等式性质,相减后两边剩下的结果,它们的位置关系是同位角,而不是因为位置恰好是同位角而导致的相等,即先知道它们相等,然后找出位置关系是同位角,前后逻辑不一样。
而在最后一步,平行的理由才是因为同位角相等,所以最后那句话应该写成“同位角相等,两直线平行”。
教学反思:
类似该学生的错误并非偶然,事实上,每一届学生中,都有不少这种错误,即使在课堂教学中想尽办法避免,依旧会犯。那么,问题的产生已经不仅仅是教师讲授,而是学生听讲的习惯。我注意到,课堂上那些中等生最容易犯这样的错误,而在课堂上,过于简单的问答让他们感觉自己已经懂了,因此不再深入思考问题,这和学霸们勤于思考正好形成对比。
所以,在课堂上,除了把问题讲清楚,更重要的是课堂练习的落实,即关注到每个学生,通过课堂上识图练习,每个学生是否真理解,需要巡视到每个学生面前。根据前面描述的重点易错人群,那么中等生无疑是课堂巡视的重点,只有在课堂上把错误消灭掉,才不会导致解题中出现的问题。
,