近年来,人们对学习哈密尔顿方程的方法进行了大量研究。尽管这些方法非常有前途,但常用的哈密尔顿方程的表示方法使用广义动量,而广义动量一般是未知的。因此,训练数据必须用这个未知的坐标系来表示,这给将模型应用于真实数据带来了困难。同时,哈密尔顿方程也有一个无坐标的表达方式,它是通过使用辛-2形式来表达的。在这项研究中,我们提出了一个利用神经网络从数据中学习辛形式的模型,从而提供了一种从一般坐标系表示的数据中学习哈密尔顿方程的方法,这种方法不限于广义坐标和广义动量。因此,所提出的方法不仅能够对哈密尔顿和拉格朗日形式的目标方程进行建模,而且还能够提取隐藏在数据中的未知哈密尔顿结构。例如,许多多项式常微分方程,如Lotka-Volterra方程,已知其存在非微观的哈密尔顿结构,我们的数值实验表明,这种结构当然可以从数据中学习。从技术上讲,每个辛2-形式都与一个偏斜对称矩阵相关,但并非所有的偏斜对称矩阵都定义了辛2-形式。在所提出的方法中,利用辛2-形式是某些微分1-形式的外导数派生,我们用神经网络对微分1-形式进行建模,从而提高了学习的效率。本次研究的主题是神经辛形式模型,我们将用这个模型学习一般坐标系下的哈密尔顿方程。
本期AI TIME PhD直播间,我们邀请到神户大学系统信息研究科计算科学专业博士生——陈钰涵,为我们带来报告分享《神经辛形式:学习一般坐标系上的哈密尔顿方程》。

陈钰涵:神户大学系统信息研究科计算科学专业的在读一年级博士生。现导师是谷口隆晴教授。于2018年获得北京信息科技大学应用统计学学士学位。博士期间的研究方向主要为深度学习与几何动力学和物理模拟技术的结合。该论文是陈钰涵作为第一作者在NeurIPS发布的文章,且被采用为spotlight。其他相关论文发表在NeurIPS,AAAI等。
1
Deep learning for physical simulation
深度学习在物理学模拟领域
Learn dynamical system 学习动力系统
- 物理学模拟具有广泛的应用
- 数据驱动方法是一种常用的加速仿真的方法
- 物理现象可用基于物理定律的微分方程表示
- 遵守物理定律保证了结果的可靠性

在计算机上对这些现象进行建模和模拟的时候,最简单的方式就是用神经网络从数据中学习代表运动方程的常微分方程右边部分,也就是我们常说的Neural ODE模型。
但由于神经网络的通用性,能量守恒等物理规律在这个模型中可能是不成立的。为了不使物理特性消失,因此把这些特性引入研究模型之中。
近年来,学者们对这些模型也进行了研究,比如Euler-Lagrange equation and Hamilton equation。
学习物理现象,同时保留物理定律
Lagrangian Neural Network (LNN)
用来学习拉格朗日动力学运动方程的模型叫做拉格朗日神经网络。
- Lagrangian system (the Euler-Lagrange equation)在这个网络中,一个神经网络被用来对拉格朗日L进行建模,并从中推导出运动方程。在拉格朗日力学中,方程是用状态变量及其时间导数来描述的。这也使得我们学习所需要的数据较为容易来准备。

- 该模型还存在一个特点,在tangent bundles切线束上定义了一个系统。
- 该模型被限制在一个特定的结构之中且该结构属于哈密尔顿方程的一部分。
Hamiltonian Neural Network (HNN)
哈密尔顿神经网络是一个比较有名的模型,这是用来学习哈密尔顿动力学运动方程的神经网络。在该网络中,一般会假设采用以下形式的模型。
- 哈密尔顿动力学系统

- 由于哈密尔顿方程本身就存在守恒定律,因此哈密尔顿神经网络也遵循能量守恒。
- 由于能量守恒定律的存在,方法在长期预测中也有良好的表现。
- 这个方法也可以被扩展为各种形式的模型,尤其是structure-preserving numerical integrators和discrete gradient method。
不过,虽然这种模型在以往的研究中也常常被应用,但是哈密尔顿方程只有在正则坐标下才拥有这样的形式。
同时,这个坐标系也取决于能量函数H,这个H是一个未知的哈密尔顿方程。所以说,这个坐标系中很难去事先准备数据,也很难将这个模型应用到实际问题之中。

在一般坐标系中,通过斜对称矩阵,哈密尔顿方程可以被转换成这种形式。但因此在一般坐标系下学习哈密尔顿动力学方程的方式是研究斜对称矩阵S(u),如果方程是按上图中的形式给出,那么就有可能显示出能量守恒定律。这种方法也被称为Skew symmetric matrix learning。但是这种方法也存在缺点,斜对称矩阵必须满足一定的几何条件。
在斜对称矩阵通过神经网络去学习的时候,模型可能不是哈密尔顿方程;在这种情况下能量可能是守恒的,但是物理规律可能是不成立的。另外,如果研究的对象是用哈密尔顿方程来进行描述的,那么学习的结果是非哈密尔顿方程,那么说明是一个效率很低的学习。

总结一下,现有学习常微分方程的基本方法是Neural ODE,但是这种方法没有物理意义,其物理定律和稳定型均得不到保证。其中分析力学提出了哈密尔顿神经网络,拉格朗日的运动方程是用位置和速度来表示的,虽然很容易准备数据,但是其几何结构却是有限的,和哈密尔顿相比能够处理的现象也是有限的。
而哈密尔顿力学可以包含拉格朗日力学不能包含的现象,但是正则坐标却被未知函数而阻碍,导致很难去准备数据。在一般坐标系中的表现,哈密尔顿方程是对斜对称矩阵学习,而在这个模型之中:能量守恒定律是可以保证的,不过需要额外的几何条件。如果学习的结果不能成为哈密尔顿方程,那么这个学习就是没有效率的。同时,其物理规律也有可能是不成立的。

2
Proposal :Neural Symplectic Form
为了解决上述问题,我们提出了以下模型,即使用神经网络来学习Neural Symplectic Form。这使得我们有可能从不局限于广义坐标和动量的一般坐标系所表示的数据中去学习哈密尔顿方程。关键是要利用哈密尔顿方程与坐标系无关的形式,毕竟之前研究的局限性在于坐标系通常会被固定为广义坐标。
然而在几何力学的研究中,方程里的ω被称为Symplectic Form。它对应于一个斜对称的矩阵,因此通过学习Symplectic Form与哈密尔顿方程,我们可以从数据中学习任何坐标系中的方程。

因此,我们提出的方法不仅能对一般坐标系中的方程进行建模,而且能够提取隐藏在数据中未知的哈密尔顿结构。由于Symplectic Form与微分形式有关,所以我们接下来要解释一下微分形式中需要的一些术语。
3
Details of the method
状态变量的移动空间被称为相位空间。考虑这样的一个相位空间M=R2N
- M中的微分0形式:从M到R的函数
- M中的微分1形式:由矢量v决定的线性函数,取决于每个点并可以被表示为矢量的内积,因此也可以被看作矢量场。
- 微分k形式是指从k个向量到实数的多个线性函数
微分形式可以定义一个微分运算,被称为外导数D,即将导数k形式转到导数k 1形式的线性映射。

说到具体的研究方法,我们首先来看一下哈密尔顿方程的无坐标系表示形式。
我们使用哈密尔顿方程的无坐标系表示法建立一个模型,这样的模型也可以用在一般的辛流形上。
微分2形式ω是一个斜对称的双线性函数,我们可以通过适当的矩阵变换得到如下的表示:
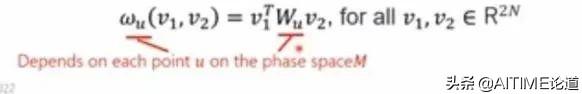
哈密尔顿方程使用了symplectic 2-form形式,可以通过这样的形式表示。

- Non-degenerate非退化:与ω对应的W矩阵有一个逆矩阵。
- Closed: dω=0意味着微分形式ω的导数为0
- u无论用什么坐标系表示都是有效的——u独立于坐标系
事实上,我们可以通过 de Rham cohomology发现,在某些假设下,1形式下θ和闭2形式下的ω有着一对一的对应关系。在提出的模型中,我们为了保证学习到的2形式是闭合的形式,需要通过学习1形式并计算其外导数来学习2形式。
这里提到的一对一的对应关系,意味着尽管微分2形式对应一个斜对称矩阵,但是并不意味着所有的斜对称矩阵都对应着微分2形式。辛形式下的Symplectic集合,是斜对称矩阵的一个子集。
从这角度来说,我们需要的是下图中黄色区域。如果我们用一般的skew matrix learning方法,最终会得到整个大的橙色部分,并不是我们希望的。
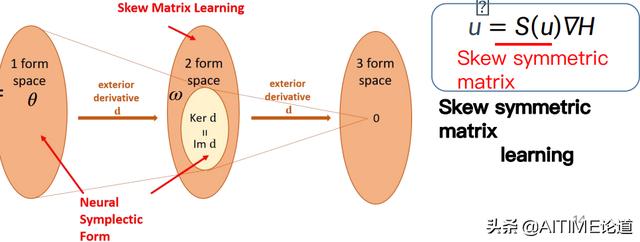
但是如果我们应用外导数D,可以直接从1形式计算得到2形式。因此,通过估计斜对称矩阵可能无法得到哈密尔顿方程,而我们的提出手法可以使其成为哈密尔顿方程。因此能量守恒之外的物理定律是有可能成立的。
到目前为止,我们已经可以从微分的形式来表示模型,同时这个模型也可以用矢量和矩阵的形式来表示。

哈密尔顿H和代表1形式θ的向量场Y分别由神经网络建模,并且通过神经网络给出的1形式θ进行自动微分,最后将微分结果放入方程得到矩阵W。
通过这种形式学习到的2形式被称作Neural Symplectic Form神经辛形式。接下来我们可以去测试一下这个模型。
Numerical experiments(mass spring model )
首先通过一个很简单的质量弹簧系统进行测试。

在下图这样一个一般坐标系上的哈密尔顿方程,q是点的位置,p是点的动量。

数据是通过位置p和p的导数,应用了1000个初始模拟值,模拟到t=5,时间增量为0.01。
对于神经网络的输入层数量,和状态变量u的维度相同;对于神经网络的输出层数量,1;Y的神经网络输出层数量也是和u的维度相同。其他设置如下图所示:

总共是用了10次训练的平均值和偏差来估计模型。

这个实验,对模型和预测结果而言并没有太大区别,Neural Symplectic依然给出了一个最好的结果,与实际轨迹没有太大区别。
Numerical experiments Lotka–Volterra model
下一个实验是带有多项式的微分方程,存在一个隐藏的辛结构。考虑到这样的模型和微分方程,可以被改写为哈密尔顿方程。但是这个方程并不是一个标准的哈密尔顿方程。而本次实验的目的是检测Neural Symplectic feature是否可以从位置的数据中提取出来。具体实验设置如下:

从结果来看,哈密尔顿神经网络的结果峰值是非常低的,因为表达式并没有以哈密尔顿方程标准形式给出。Node的节点和峰值越来越低,表明能量在逐渐丧失。

可以从上图数据中看出,结果图像是要比真实的峰值低一些的。这是因为斜对称矩阵寻找到了更宽的领域,除了能量守恒定律也没有其他的物理定律可以建立。而我们提出的Neural Symplectic Form几乎给出了真实的轨道,因此该方程隐藏的辛结构可以通过我们的方法被有效提取出来。
Numerical experiments(double pendulum)
实验配置如下:

从广义动量方程来看,这个方程较为复杂,如果我们事先不知道这个方程就很难去准备数据。

从下图实验结果可以看出,模拟的振幅非常小,哈密尔顿神经网络没能够准确的预测出轨迹。因为我们直到q和q的导数但不知道p,所以这是个失去了作用的模型。
拉格朗日神经网络失败的原因则可能是数据的用量较少。对于我们提出的模型,峰值比实际的轨迹略高,但震荡速度似乎是正确的 。对于NODE模型,一定程度上与实际规矩是匹配的,但是在长期的预测中并没有给出正确的结果。

从下图可以看出,只有我们提出的Neural Symplectic Form是稳定的形式,并在持续震荡。

Numerical experiments
Error in time differentiation

从时间导数和误差数值来说,在大多数时间下我们的提出的方法具有较好的性能且误差较小。
Error of energy

对于能量误差,Node模型与斜对称矩阵在短时期内具有良好的表现,但是这两个模型在长时间的实验中全部失败。
4
Future task
我们还进行了一个实验,从图像中学习其动态,预先训练了一个从图像中提取特征的autoencoder,并应用哈密尔顿神经网络和Neural Symplectic Form去学习这些特征的动态。
Neural Symplectic Form给出的derivative loss是一个非常小的结果,哈密尔顿神经网络结果的最后4幅图像存在noise,意味着其潜在空间误差较高。

下图是与图像正确对应的空间是蓝色部分,而图像之所以没有很好还原的原因在于预测到了白色部分。

但是这只是个初步的测试,因为在实验中还存在着许多缺陷。比如实验中性能仍取决于autoencoder的结构,所以我们还需要更彻底的调查。
5
Conclusion
Neural Symplectic Form神经辛形式
- 基于一个几何和独立于坐标系之外的的哈密尔顿方程。
- 用神经网络对微分1-形式进行建模,保证了学习到的2-形式是封闭的。因此,学习到的模型总是哈密尔顿系统
- 除了能量守恒之外,其他物理定律也成立
- 应用范围广
- 也适用于拉格朗日系统(以位置和速度表示的数据)
提醒
论文题目:
Neural Symplectic Form: Learning Hamiltonian Equations on General Coordinate Systems
论文链接:
https://openreview.net/pdf?id=4h4oqp-ATxb
,




