圆的面积公式:
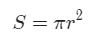
圆的周长公式:
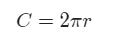
如果对圆面积公式的自变量r求导,则会发现
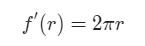
与周长公式完全相同,这是为什么呢?
对于一个半径为1的圆的面积,等同于底为2π(6.28),高为1的三角形面积。

我们可以这样理解r的变化对于圆面积的变化:
每当r增加一个很小的增量Δr(Δr 0),圆的面积就增大一圈:

对应的三角形面积也增加一层:

圆增加的圆和三角形增加的层,都可以看成增加了一个2π(t Δt)的圆或线,于是无穷个这样的圆(总半径和度为1)叠加成为该圆的面积。
所以我们可以用定积分来求圆的面积(半径为1的圆):
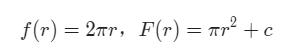
F(r)为f(r)的原函数
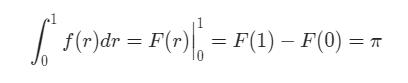
当数学引入微积分后,我们就需要理解“无穷个叠加成有限个”这个思想。
如:一个长度为1的线段是由无数个点所构成的;一个体积为1的正方体是由无数个面积为1的长方形构成的。
这个也可以这样想:无数个低维物体构成一个有限的高维物体。
点是一维的,线段是二维的;
长方形是二维的,长方体是三维的。
对于这个理解,以前的数学家们也是花了很长的时间,比如著名的“追乌龟(阿基里斯悖论)”:
阿基里斯(又名阿喀琉斯)是古希腊神话中善跑的英雄。在他和乌龟的竞赛中,他速度为乌龟十倍,乌龟在前面100米跑,他在后面追,但他不可能追上乌龟。因为在竞赛中,追者首先必须到达被追者的出发点,当阿基里斯追到100米时,乌龟已经又向前爬了10米,于是,一个新的起点产生了;阿基里斯必须继续追,而当他追到乌龟爬的这10米时,乌龟又已经向前爬了1米,阿基里斯只能再追向那个1米。就这样,乌龟会制造出无穷个起点,它总能在起点与自己之间制造出一个距不管这个距离有多小,但只要乌龟不停地奋力向前爬,阿基里斯就永远也追不上乌龟!
“乌龟” 动得最慢的物体不会被动得最快的物体追上。由于追赶者首先应该达到被追者出发之点,此时被追者已经往前走了一段距离。因此被追者总是在追赶者前面。”

这个悖论就是将追上的总距离无数细分:10 1 1/10 1/100 1/1000…...
《庄子·天下篇》中也提到:“一尺之棰,日取其半,万世不竭。”
这个也是将一个有限长度的棰无限细分:1/2 1/4 1/8 1/16……
,




