【题目呈现】
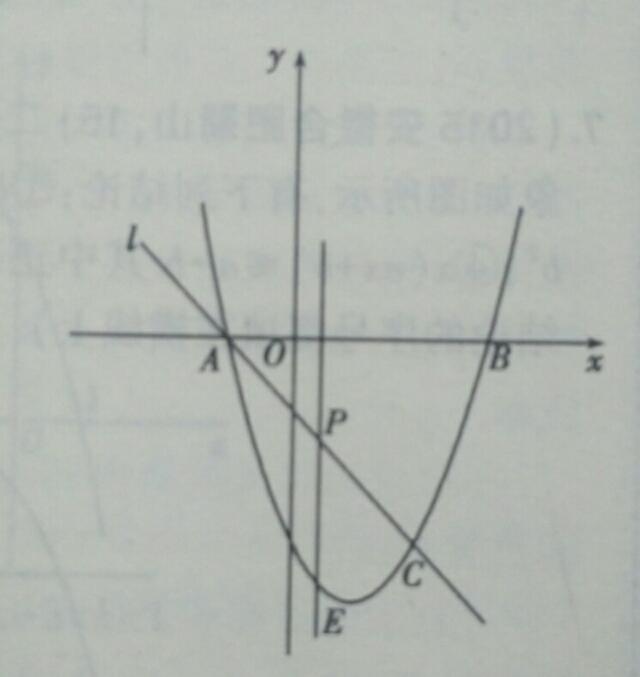
如下图,抛物线y=X²一2x一3与x轴交于A、B两点(A点在B点左侧),直线L与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过点P作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使得以A、C、F、G为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的F点坐标;如果不存在,请说明理由.
【分析】
(1)A、B两点的坐标,令抛物线y=0,解方程可得,∵C点横坐标已知,代入抛物线可得C点纵坐标,再用待定系数法求直线AC的表达式.
(2)由于PE平行于y轴,P、E两点横坐标相同,设出其中一个点的横坐标,纵坐标分别用相应的函数关系式表示,进而表示出线段PE长度的关系式,求出最大值.
(3)由于A、C两点确定,那么以线段AC为边,为对角线分类讨论。
【答案与解析】
解:(1)令抛物线y=x²一2x一3的y=0,解得x1=一1,x2=3,∴A(一1,0),B(3,0),将C点的横坐标x=2代入y=X²一2X一3,得y=一3,∴C点坐标为(2,一3),设直线AC的解析式为y=Kx b(K、b为常数且K≠0),代入A(一1,0),C(2,一3),得①0=一K b且②一3=2K b,解得,K=一1,b=一1,∴直线AB的解析式为y=一X一1.
(2)设P点的横坐标为x(一1≤x≤2),由于PE∥y轴,E在抛物线上,∴P点坐标为(x,一x一1),E点坐标为(x,x²一2x一3),∴PE=(一X一1)一(X²一2x一3)=一x² x 2=一(x一1/2)² 9/4,∴当x=1/2时,PE取得最大值为9/4.
(3)在x轴上存在点F,使得以点A、C、F、G为顶点的四边形为平行四边形,如下图

①当AC为对角线时,只能是AF∥CG,设抛物线于y轴的交点为D,D点坐标为(0,一3),∵C点坐标为(2,一3),∴CD∥AF,设此时F为F1,G为G1,则G1点与D点重合时符合条件,∵AF1=G1C=2,∴F1点坐标为(1,0).
②当AC为边,AF2∥G2C,且AF2=G2C时,在x轴下方,G2点与G1点重合时符合条件,∴点F2为(一3,0);当AC为边AG为边在x轴上方,到x轴距离为3存在两个G点,相应的在x轴上存在两个F点,令抛物线y=x²一2X一3=3,解得x=1±√7,不妨设点G3坐标为(1十√7,3),点G4坐标为(1一√7,3),∵对角线G3C的中点(3/2 √7/2,0),也是对角线AF3的中点,点A(一1,0)∴点F3坐标为(4 √7,0),同样,对角线G4C的中点(3/2一√7/2,0),也是对角线AF4的中点,∴点F4的坐标为(4一√7,0).
综上所述,符合条件的点F的坐标为F(1,0)或F(一3,0)或(4 √7,0)或(4一√7,0).
另外,用点的坐标平移求F4,F3两点坐标也比较简单,由于点A(一1,O),向右平移3个单位,再向下平移3个单位到C(2,一3)点,∴G3(1 √7,3)点向右平移3个单位,再向下平移3个单位得点F3(4十√7,0),G4(1一√7,3)点向右平移3个单位,再向下平移3个单位得点F4(4一√7,0).
【反思】
对于平行四边形存在性问题,有三定,一动;两定,两动;一定,三动等几种情况,尤以第二种情况多见,运用分类讨论的思想,结合三角形全等,勾股定理,中点坐标,以及平移等知识方可解决。
感谢大家的关注,转发,点赞,交流!
,