灵机一动
数学是思维的体操,很多数学问题的解答往往就闪现在你的灵机一动之中。本栏目精选数学中的好题、趣题,以及最能锻炼数学思维的题呈现给大家,希望给你带来思考的乐趣。
本期问题来了
NO. 202
手机密码

小明五次输入四位数的手机密码均有误,但是每次输入的密码中有两位数字正确,位置都不对。现求小明正确的四位数手机密码?
五次手机密码分别是:6087 5173 1358 3825 2531
★ 右下角写留言或点击左下角的阅读原文进入答题页面,直接在帖子后面回复你的答案。
★ 如果想不出来,可以转发朋友圈向朋友求助哦!答案将在下期公布。
★ 公众号中回复题友会申请加入题友会微信群,与题霸们一起刷题。
上期问题回顾
NO. 201
循环报数

2016名学生站成一列,从排头到排尾报数,报平方数的人出列。报完一遍后再从排头到排尾重新报数,报平方数的出列……上述过程不断进行,问最后一个出列的第一次报数时报的是几号?
分析与解答
答案:1981。
下面这个三角形数表经常会出现在初中或高中数学平常的练习中,考得简单一点可能会问你第n行的最后一个数是多少?聪明的同学很快就会发现这个三角形数学的右边这条边上的数都是平方数。
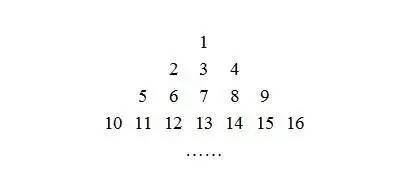
其实上述三角形数表蕴含着一个非常重要的公式,这个公式就是:
也就是前n个奇数的和为n²。这个看似没什么用武之地的数表在这里将发挥大作用,把这道题和这个三角形数表联系起来的纽带就是平方数。
本期循环报数的问题可转化为在三角形数表中划数的问题:在三角形数表中,先划掉平方数,然后对剩下的数按从小到大的顺序重新编号,把编号为平方数的数划掉,依次重复此操作直至剩下最后一个数,求最后剩下的这个数在原三角形数表中是什么数。
当然,为了寻找到破解该问题的钥匙,我们先从小处着手,并且只考虑学生数恰好为平方数的情况。
下面的步骤,建议你拿出纸和笔,用笔在纸上画一画。

对于9个数、16个数、25个数的三角形数表,根据划数规则,如上图所示,第一次划掉的都是三角形最右边斜边(红线)上的数,第二次划掉的是靠近中间蓝线上的数,接下来都是依次划掉一条红色斜线上的数,然后再划掉一条蓝色竖线上的数。最后剩下的是最后一行中间的那个数,即图中用绿色圆圈标记的数。
推广到一般情形,有结论:对于有n²个数的三角形数表,按照上述划数规则,最后一个被划掉的数是原三角形数表最后一行中间的那个数。
对于以上结论,是由归纳法得到的,对于由归纳法得到的结论是不能保证一定正确的,作为数学的严谨性来说,应该予以证明,在这里我将在文末以附录的形式给出,你也不妨思考一下如何证明。下面我们继续讨论该问题。
上述结论只是结出了n²个数时的答案,对于非平方数,答案又是什么呢?以三角形数表中的最中间一列数(指1,3,7,13,…那一列数)为界线,如果最大的数位于界线右侧,则最后划掉的数为最后一行最中间的那个数;如果最大的数位于界线左侧,则最后划掉的数为最后一行最左边的那个数。(该结论留给各位题友自己去探索)
有了以上的分析和探索,我们很容易知道,对于2016个数的情况,最后一个被划掉的数1981,也就是本期问题的答案。
注:本题也可以用正方形数表来做,参见题友解答精选中邹家俊老师的解答。
题友解答精选
◎题友 @邹家俊的解答:

◎题友 @卞爱华的解答:
最后出列的是1981号。联想到公式1 3 …… 2n-1=n²,将所有人排成方阵。容易证明,第1次出列的是第1排,第2次出列的是对角线,这个过程将循环出现。可以看出,最后一个出列的,要么是左下角n² 1,要么是右下角n² n 1。本题的情况是右下角44² 45。(配合上述图形理解)
◎题友 @乐乐的解答:
最后出列的是1981号。我们把这个过程倒过来看,最后一次出列的是当时的1号,倒数第二次时能留到最后的是当时的2号,倒数第三次时能留到最后的是当时的3号,倒数第四次能留到最后的是当时的5号,……不难看出,倒数第2k次能留到最后的是当时的k^2 1号,倒数第2k 1次能留到最后的是当时的k^2 k 1号。回到本题,2016人可以经过89轮报数,初始位置为44^2 44 1=1981的人最后退出。
附录:
本附录将证明文中提到的推广到一般情形的结论:对于有n²个数的三角形数表,按照上述划数规则,最后一个被划掉的数是原三角形数表最后一行中间的那个数。
证明:根据三角形数表的排列律可知,第k行最后一个数为k²,第一个数(即最左边那个数)为(k-1)² 1=k²-2k 2,最中间那个数为(k² k²-2k 2)/2=k²-k 1,最中间左边第一个数为k²-k。

对于有n²个数的三角形数表,第一次我们划掉的是三角形右边斜边上的数,共有n个,此时还剩下n²-n个数。如果将剩下的数重新编号,现在我们来考虑中间那一列的左边第一列的数,原来的编号为k²-k,因为删掉了三角形右边斜边上的数,重新编号之后为k²-k-(k-1)=(k-1)²,是一个平方数,所以第二次划数时应该全部划掉,共有n-1个。经过两次划数之后,还剩下n²-n-(n-1)=(n-1)²。剩下的数正好组成一个(n-1)²的数表,我们又可以按上述规则分别把三角形右边斜边上的数以及中间一列的左边第一列数给划掉,依此进行下去,最后将只剩下第n行最中间那个数k²-k 1。
点击下方“阅读原文”开始答题
↓↓↓
,




