在理科数学的高考中,复数这一部分的考察似乎是被边缘化了,和其他部分联系不大。当然了,这可能是出于考纲对这一部分内容的难度限制。回忆高中所讲的有关复数的知识,也无非就是复数的相关概念以及运算法则。
但是在高中所讲的这些内容中,复平面这一概念对于复数是相对关键的。它是一个舞台,复数加减乘除等运算带来的各种变化,都将在这个舞台上呈现。

回顾向量的坐标的定义。向量的坐标定义为把这个向量平移到起点与坐标原点重合的位置时向量终点的坐标。因此,使用复数乘法同样可以将向量旋转。方法是一样的。例如将a=(x,y)逆时针旋转90°得到b,算出(x yi)i=-y xi,于是b=(-y,x)。在解析几何中涉及到两垂直向量数量关系的问题,都可以使用这种方法。下面以两个例子具体说明。
例题1:
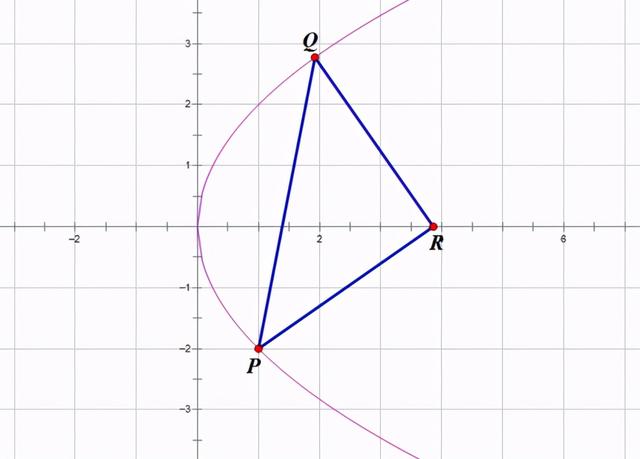
已知抛物线C:,设P(1,-2),Q为抛物线C上的两个不关于x轴对称的点,判断在x轴上是否存在点R使得ΔPQR是以R为直角顶点的等腰直角三角形?若存在,求出点R的坐标;若不存在,说明理由。