我们知道可以有无数个圆经过平面上的一点A。

也很容易想到,经过平面的上的两个点(A,B)可以作无数个圆。

那么经过两点的圆和经过一点的圆有什么不同?是的,所有经过两点的圆的圆心都会在线段AB的中垂线上。

中垂线也叫“垂直平分线”:
一条垂直于线段(AB)的且平分该线段(AB)的直线,叫中垂线。
中垂线还有一个很重要的性质:
中垂线上点到A点的距离和到B点距离相等,即CA=CB,DA=DB,EA=EB

我们可以使用勾股定理来证明这个:

那么经过三个点能有几个圆呢?答案是1个,这就是三点确定一个圆。

在平面中三个点A,B,C,连接任意两条线段(AB,BC),分别做两条中垂线相交与O点,∵ OA=OB,OB=OC,∴OA=OB=OC,即点O为所作圆的圆心。以O为圆心,OA,OB,OC任意线段的长度为半径作圆,即可得到一个经过三点的圆,且这个圆只有一个(因为两条中垂线只有1个交点)。
我们发现“三点确定一个圆”跟另外一个几何图形很相似——三角形。三角形也是通过三点来确定,并且他们都共同遵守一个限制条件:三点不能在一条直线上。
三个不在一条直线上的点能确定一个圆和一个三角形。
(想想是什么原因?)
既然圆和三角形相似,那么可以确定三角形必然会有一个外接圆。
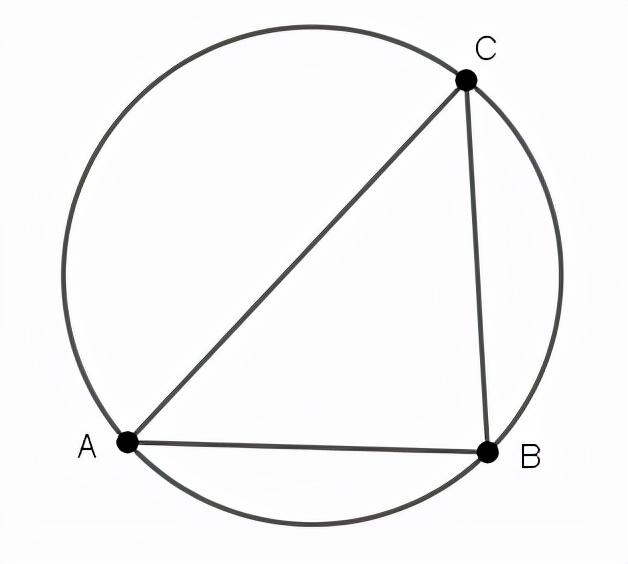
三角形外接圆就是经过三角形三个顶点的圆,而ΔABC是这个圆的内接三角形。
在一些几何题中经常会遇到一个ΔABC的外接圆,但没有给出圆心,我们可以通过作其中两条边的中垂线,它们的交点(O)就是该外接圆的圆心。

通过这个知识点我们还可以学会“三角形的三条中垂线交于一点”的证明方法:
因为我们知道点O到A,B,C的距离都相等,即AO=BO=CO,对于线段BC,O点到点B和点C的距离相等,那说明点O必然在线段BC的中垂线上。
由于点O同时在三条中垂线上,那么这三条中垂线交于一点。
有些同学对这点有点难理解——为什么一个点同时在三条直线上,就说明这三条直线交于一点?
我们知道同一平面内的三条直线会有三种状态:
① 相互平行,② 相交于一点,③ 相交于三点
只有第二种情况是一个点同时在三条直线上。
同样,对于同一平面的两条相交直线,我们可以说:
① 这两条直线相交于一点O
② O同时在这两条直线上
这两种说法是等价的。
,




