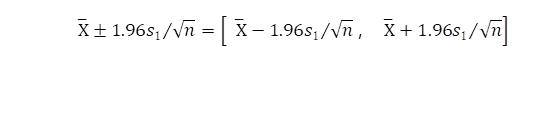置信区间统计学操作（统计学系列区间估计）

点估计与区间估计

在上一篇文章---"两个重要统计量——均值和比率“里，我们介绍了用样本均值`x估计未知的总体均值`a，这个`x是一个数（而不是一个范围），因此这种形式的估计叫作点估计。

另外，我们还介绍了方差和标准差，我们认识到用`x估计`a是有误差的，而标准差从平均的意义上反映了误差幅度，因此，如果我们以标准差作为衡量散布度的一个单位，把未知的总体均值`a估计在（`x -一个标准差）的范围内，这种形式的估计就叫作区间估计，因为它把未知值估计在一个范围内。

分布密度曲线与分布密度函数

方差是总体中各个体指标的散布程度的综合刻画，它在一定意义上也有助于刻画样本均值在估计总体均值时的精度。但是，由于总体中个体指标值的分布可能是均匀的，可能是“两头大，中间小”或“两头小，中间大”等，这种分布上的差异，将导致区间（`x -一个标准差）的可靠程度有很大差异。

对于分布我们将做如下介绍。设一总体包含N个个体，其指标值分别为a₁ , …, a_N。所谓“指标值”，就是个体的某种性质的数量刻画，而这种性质是与我们所研究的问题有关的。设我们从总体中随机抽出一个个体，并以X记其指标值，常把X称为随机变量。当把相近的指标值结成一组，并给出组的比率，我们将得到如下的分布的直方图。

在许多实际问题中，总体所含个体数或者是为数极大的，或者在理论上说是无穷大的。则X这个变量原则上有无穷个可能值，我们可以采用“以有限逼近无限”的方法，在X的取值无限制地增加下，直方图在理论上愈来愈接近一条曲线，如下图（b）所示。

从理论的观点看，这条曲线给出了总体指标分布的一个完整的描述，即称为总体指标的分布密度曲线。如果在平面上引进直角坐标系，分别以x和y记一个点的横坐标和纵坐标，则一条曲线可用一个函数y=f(x)去刻画，这个f(x)也就称为总体指标的分布密度函数。

上图即为分布密度曲线与函数。并具有以下三条基本性质：

1） 这条曲线全在横轴的上方；

2） 总体中，指标值介于a和b之间的个体所占的比率，等于图中斜线部分的面积；

3） 曲线与横坐标轴之间围成的面积等于1。

正态分布

下图曲线所代表的的函数就是标准正态密度函数。确切公式为：

这条曲线关于y轴对称，在x=0处达到它的最高点，从这最高点出发，往正负两个方向都下降到横轴上去。这条曲线与横轴围成的面积为1，而且：

在-1到1之间的面积为0.683；

在-2到2之间的面积为0.956；

在-3到3之间的面积为0.997；

在-1.960到1.960之间的面积为0.950；

在-2.576到2.576之间的面积为0.990；等。

服从标准正态分布的总体，其指标值X的均值是0，方差是1。常记为X~N(0,1)。若X服从正态分布，但其均值为a，方差为σ^2，则记为X~N(a,σ^2)，且(X-a)/σ~N(0,1)。(X-a)/σ称为把指标X“标准化”。

正态分布是统计学中最重要的一种分布。

1） 实用方面看，在许多问题中，总体指标的分布都很接近于正态分布，例如一群人的身高、体重、血压，重复测量某个量（如称物）所得到的结果，大批生产一种产品时，其某项质量指标等等。

2） 正态分布的统计问题在理论上解决得很彻底且便于应用。它具有许多优良性质，列举两个如下：

(1)样本均值的正态性。设总体中个体的某项指标X~N(a,σ^2)。现在给定一个自然数n，从该总体中随机地抽出n个样本，结果记为X₁,…,X_n。以`x记样本均值，则`x仍服从正态分布，

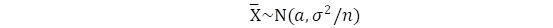
(2)若指标X服从正态分布N(a,σ^2)，A和B为两个常数，A不等于0。 令Y=AX B，则指标Y仍服从正态分布，确切地说，有

区间估计

前文我们说到，标准差可以在平均意义上反映样本均值的精度，但是从区间估计的角度看，仅凭标准差已不能给出什么带普遍性的结论，而必须结合指标的分布去考察才行。

由于在实际问题中分布是各式各样的，这就注定了不可能提出一种简易可行、处处适用的方法。幸好，上文提到的正态分布有很大的普遍性，因此，针对这种分布提出的解法（即得到给定置信系数的区间估计,置信系数：把未知的均值估计在某一区间内，其正确的机会），有相当程度的普遍意义。另外，对一般的（可以是非正态的）分布而言，只要样本大小足够大，基于正态分布的解法仍能适用，只是从理论上说，这种解法是近似地而非确切的。下面分三种情况介绍相应的解法：

1） 总体中个体指标X的分布是正态的，即X~N(a,σ^2)，其中方差已知，要估计的是均值.

从总体中抽取了n个样本X₁,…,X_n，则样本均值

，于是标准化变量

服从标准正态分布N(0,1)

我们知道标准正态密度曲线在-1到1之间的那部分面积是0.683（即总体中指标值介于±1之间的那些个体，在总体中所占比率为0.683）。根据这个结论，不等式

实现的机会为0.683。以上不等式可改写为

未知的a落在该区间内的置信系数为0.683。

同理，我们可以得到一系列的区间估计：

以上，可以看出，置信系数取得越高（即对估计越有把握），相对应付出的代价就是估计区间变大了。

一旦取定了一个置信系数，则区间长度也定下来了。

例如，取置信系数为0.95，则区间长度为

如果l太大，则估计很粗糙并且实际意义也很小。我们不能靠牺牲置信系数来降低这个长度，因为这会使估计变得很不可靠，用起来有危险。解决办法是选择适当的样本大小n。由上面求l的式子可知，如果我们指定区间之长不能超过某个限度l₀，则n必须满足：

2） 总体中个体指标X的分布是正态的，即X~N(a,σ^2)，其中方差未知，要估计的是均值.

例如，取置信系数为0.95，在方差已知的情况下，则用区间估计

，现在由于方差未知，则这区间的端点算不出来。一种解救办法是用样本的标准差s，经修正为无偏估计的s₁作为σ的估计以代替

得出的区间估计为

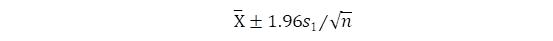
由于我们对上面区间估计的计算是根据

服从标准正态分布N(0,1)这个性质的，用s₁代替后，由于s₁本身就是从样本算出的，它有随机性而非常数，故代替后的变量已不再是服从标准正态分布。它的分布是英国统计学家哥色特在1908年发现的，称为自由度为n-1的t分布，常记为t_n-1。此分布的形状与标准正态分布很相似，在外表上无法区别，理论上可以证明，当样本大小n愈来愈大，t分布愈来愈接近于标准正态分布。大样本的情况将在接下来介绍，但针对总体服从正态分布，方差未知，又是小样本的情况，t分布将给我们的区间估计带来帮助。

由于分布t_n-1已不是标准正态分布，与置信系数0.95,0.99和0.90等对应的，已不是前面指出的1.96,2.576和1.645，而是比较复杂，因为它与自由度n-1有关。我们约定用t_n-1（置信系数）记相对应的系数，修正后的区间估计是

3） 设有一个无限总体（包含无穷个个体），或包含极大数目个体的总体。从总体中抽取了n个样本X₁,…,X_n，要用它对均值作估计。

统计学的理论证明了一个极重要的事实：不论原总体的分布如何，只要n很大且n/N很小，则变量

仍近似地有正态分布，甚至在把用其估计值s₁代替时，这个性质仍成立：

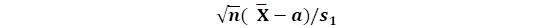
近似地服从N(0,1)。在统计学上，把这个重要的理论结果叫作“中心极限定理”。在这个约定的前提下，用前面的方法，就可以求出的区间估计（置信系数为0.95）为

,