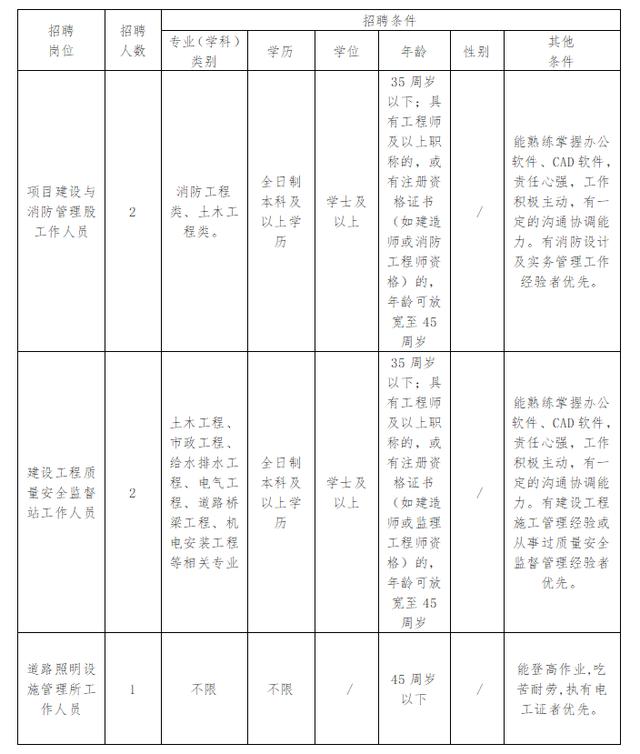
一道初中几何题-求三角形的周长
在三角形ABC中AB=12, BC=24, AC=18, BO平分角∠CBA, CO平分角∠ACB, O是角平分线的交点, 如果MN平行于BC, M和N在三角形ABC的边上,求三角形AMN的周长是多少。

解:
由于BO和CO各自是角B和角C的平分线, 因此
∠MBO=∠OBC
∠NCO=∠BCO
由于MN平行于BC, 所以
∠MOB=∠OBC,
∠NOC=∠BCO
因此
∠MBO=∠MOB
∠NOC=∠NCO
所以MB=MO, NO=NC,
因此三角形AMN的周长=AM MO NO AN
=AM MB AN NC
=AB AC
=12 18
=30
由此可见三角形AMN的周长与BC的长短无关,只要BC满足三角形三边的关系,总有三角形AMN的周长为AB AC之和的长度。
这道题如果不仔细观察盲目地去解容易走入误区。一般常规的想法是三角形AMN相似于三角形ABC,只要求出相似比就可以求出三角形AMN的周长,但这样将很繁琐。
,