题目:轨道AB固定在竖直平面内,C,D是倾斜传送带上下两转轮与皮带的切点,传送带下段紧接着斜面,斜面底端有一弹性板E。已知倾斜传送带和斜面与水平面的夹角都为30°,传送带CD间距离为4m,斜面DE长2m。一质量为m=0.2kg的小滑块在A点释放后,从轨道末端B水平抛出,从C点以Vc=5m/s的速度沿CD方向进入传送带。滑块与弹性板碰撞前后速度大小不变,滑块与传送带和斜面间的滑动摩擦因数均为7√3/15.
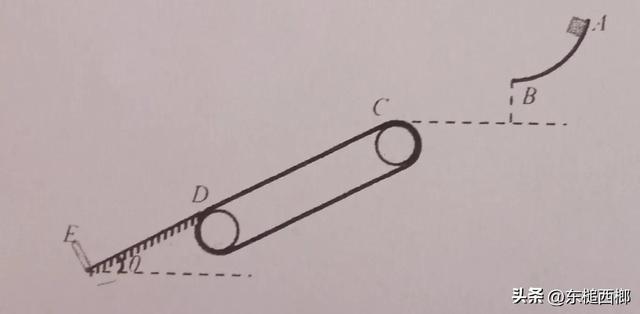
⑴求滑块从B运动到C的时间t。
⑵若传送带静止不动,则滑块与弹性板碰撞时的速度大小是多少?反弹后能上滑的最大距离x是多少?
⑶若传送带逆时针匀速运行的速度大小为v,请写出滑块与弹性板碰撞后能上滑的最大距离x'与v之间关系式。
思路:
⑴滑块从B点到C点,做的是平抛运动,Vc方向与传送带方向一致,根据角度关系可求出竖直分速度Vcy,进而根据V=at,求出t。
⑵因为传送带和斜面与水平面夹角相同,且动摩擦因数相等,因此这一问,把它们看成一个大斜面,沿斜面向下做匀减速直线运动,反弹后,继续做匀减速直线运动,令末速度为零,可求出x的值。
⑶传送带速度V需要分情况讨论,找到临界点:①当物块运动到D点时,与传送带共速时。②当物块运动到D点前,一直在做匀加速运动。
详解:






