各位朋友,大家好!今天是2020年9月16日星期三,数学世界将继续为大家分享小学各年级的数学竞赛试题以及思考题。今天我们讲解一道有关求阴影部分面积的小学数学竞赛题,此内容属于综合能力提高题,对于多数学生来说有比较大的难度,我们并不要求所有的学生都能够掌握这样的解题方法。数学世界在此分析与解答这些题目,希望能够激发学生学习数学的兴趣,并且给大家的学习有一些帮助!
例题:(小学数学竞赛题)如图,在一个梯形内有两个三角形的面积分别为10平方厘米和12平方厘米,已知梯形的上底长是下底长的2/3,求图中阴影部分的面积是多少平方厘米?
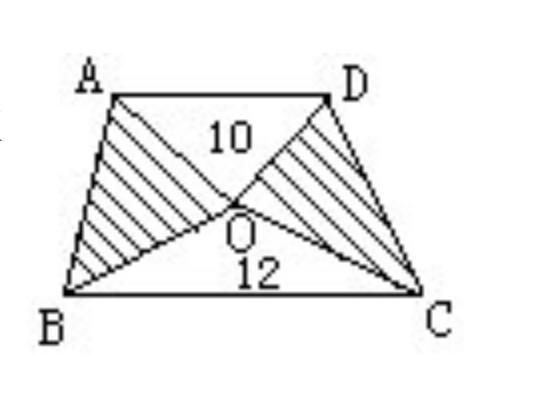
这道题要求的是阴影部分的面积,而阴影部分是由两个三角形组成,但是这两个三角形的底和高都是没有办法求出的,所以不可能运用三角形的面积公式进行解答,只能考虑采用图形面积加减的方法来解决问题。很多学生看完此题后,就感觉太难了,不知如何思考。对于这样的题目,他们一般都是空着不做。接下来,数学世界就与大家一起来完成这道例题吧!
分析:根据条件,阴影部分并不是一个图形,考虑采用图形加减法,由图可知,阴影部分的面积=梯形ABCD的面积-两个空白三角形的面积。由此可知只要求出梯形ABCD的面积即可。
下面,我们就来想办法求梯形ABCD的面积。因为梯形的上底长是下底长的2/3,所以AD:BC=2:3。又因为S△AOD:S△BOC=10:12=5:6,所以△AOD的高h1与△BOC的高h2的比可以求出,接着求出△AOD的面积与梯形ABCD的面积之比,进而求得梯形ABCD的面积,于是问题可以得到解决。下面,我们就按照以上思路解答此题吧!
解答:因为梯形的上底长是下底长的2/3,
所以AD:BC=2:3,
因为S△AOD:S△BOC=10:12=5:6,
所以△AOD的高h1与△BOC的高h2的比为
(注:由于是求比,可以直接把面积和底长看成对应的数字)
h1:h2=(5×2÷2):(6×2÷3)=5:4,
所以△AOD的面积与梯形ABCD的面积之比为
(5×2÷2):[(2 3)×(5 4)÷2]
=5:(45/2)=2:9,
于是梯形ABCD的面积是:
10×9/2=45(平方厘米)
阴影部分的面积是:
45-(10 12)=23(平方厘米)
答:图中阴影部分的面积是23平方厘米。
(完毕)
这道题主要考查了三角形和梯形的面积公式的灵活应用。解答此题的关键是:由三角形面积的比和底长的比得出高的比,这也是此题的难点。温馨提示:朋友们如果有不明白之处或者有更好的解题方法,欢迎大家在下面留言讨论。
,




