
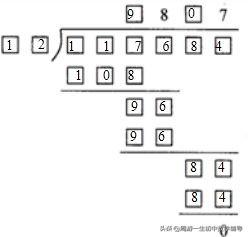

列竖式进行多位数除以多位数计算时,相信大家都经常遇到过这样一种尴尬局面:第一步试商时,该商似乎是1,但仔细一看又不能是1,只能退一位定为9,接着麻烦就来了。
比如,61789÷637,列竖式试商时,617÷637的商多么希望是1啊,但因商不足1,不得不退一位再对6178÷637进行试商,结果为9,接下来最令人心烦意燥的9乘以637开始了……,好不容易算出9×637=5733,真是费时费力又费神,尽管算好了,但还是总担心算错了,又只好不厌其烦地算一遍这才放心.

如何缓解这种尴尬,摆脱计算繁杂的困境呢?下面的方法也许对你有所帮助.
首先,我们依然是按照原来认知的多位数除法的思路,除数是三位数,试商时自然是先考虑被除数的前三位数617除以除数637,此时商虽然不足1,但已是非常接近于1了,此时如果把商定为1,结果会怎么样呢?
显然,把617÷637试商为1,接着完全可以摆脱9×637的困境,但接下来61789减去63700不够减了怎么办?这一点当然难不倒学过负数的初中生,大家马上能算得61789-63700=-1911,而对于小学生来说,只需要记住:61789减去63700不足1911,而1911÷637=3,因此,最后只需要把61789÷637所得的试商100再减去3就可以了。
即61789÷637=100-3=97。

而对于初中生来说,只需要进行如下的操作就行。
61789-637×100=-1911,
这表明61789÷637所得的商不足100,接下来只需要再用这个差-1911除以637,易得余商为-3,即-1911÷637=-3.
最后,只需要把试商100加上余商-3,结果97就是61789÷637的商.
上述算法过程如下:
61789-637×100=-1911,
-1911÷637=-3,
所以61789÷637=-3 100=97.
事实上,这种算法的依据就是:A÷B=(A- B×n)÷B n(n为首位外,其他数位上的数均为0的整数),其中n称之为试商,(A- B×n)÷B称为余商,计算结果为:余商 试商.
这里的试商n的确定既要根据被除数A的大小,也要考虑与除数B相乘时的感受,首要原则要注意方便计算B×n.否则一切都是浮云.
一般地,试商时先估算一下被除数是除数的几万倍?你千倍?几百倍?几十倍?然后选择最接近的"几"。
例如,计算:217404÷732.
显然,被除数约为除数的2、3百倍,易知更接近于300倍,因此,试商为300,
用被除数217404减去732×300,得:-2196,
用-2196除以732,得余商为:-3,
把余商-3加上试商300,得297.
所以217404÷732=297.
计算过程如下:
217404-732×300=-2196;
-2196÷732=-3;
所以217404÷732=-3 300=297.

这种算法也可以象传统的列竖式相除那样进行,所不同的是试商时不按原来的套路(保证试商与除数相乘不大于被乘数)进行,而是按我们"理想"的商确定,当试商与除数的积大于被除数时,余数不足,此时在试商后面补上相应个数的0;最后再减去不足余数与除数的商。
一般地,确定减去除数的倍数时,先看除数是几位数,然后再看被除数相同的前几位数最接近的是除数的多少倍(假设为m倍,m为),选择最接近的,又容易计算的倍数.再看以下几例:
例1 计算:9875÷25.
解:因为被除数接近于除数的400倍,
所以9875-25×400=9875-10000=-125,
-125÷25=-5,
所以9875÷25=-5 400=395.
例2 计算:6566÷67.
解:因为被除数接近于除数的100倍,
所以6566-67×100=-134,
-134÷67=-2,
所以6566÷67=-2 100=98.
例3 计算:23616÷82.
解:因为被除数接近于除数的300倍,
所以23616-82×300=23616-24600=-984,
-984÷82=-12,
所以23616÷82=-12 300=288.
例4 计算:73284÷372.
解:因为被除数接近于除数的200倍,
所以73284-372×100=-1116,
-1116÷372=-3,
所以73284÷372=-3 200=197.
例5 计算:48375÷125.
解:因为48375接近于125的400倍,
所以48375-125×400=-1625,
-1625÷125=-13,
所以48375÷125=-13 400=387.
例6 计算:499992÷502.
解:499992-502×1000=-2008,
-2008÷502=-4,
所以499992÷502=-4 1000=996.
例7 计算:58904÷199.
解:58904-199×300=-796.
-796÷199=-4,
所以58904÷199=-4 300=296.
从以上几例可见,这种算法与传统算法比较,其优越性在于可以克服第一步试商时"多一不足,少一繁杂"的尴尬局面和困境.
在A÷B=(A- B×n)÷B n中,记(A-B×n)=C,进行C÷B计算时,如果依然觉得繁杂,可以再根据这种方法将C减去B的某个倍数m,最后将各次得到的余商、试商相加.
例8 计算9618824÷3254.
解:被除数接近于除数的3000倍,
9618824-3254×3000=-143176,
-143176接近于3254的-40倍(注意:这里试商为-40),
所以-143176-3254×(-40)=-13016,
-13016÷3254=-4,
所以9618824÷3254=-4-40 3000=2956.
例9 计算:6779815÷679.
解:6779815-679×10000=-10185,
-10185-679×(-20)=3395,
3395÷679=5,
所以6779815÷679=5 10000-20=9985.
例10 计算:79764168÷7986.
解:79764168-7986×10000=-95832,
-95832-7986×(-10)=-15972,
-15972÷7986=-2,
所以797764168÷7986=10000-10-2=9988.
说明:本方法适用于被除数接近除数整十、整百倍、整千倍之类的相除。
,




