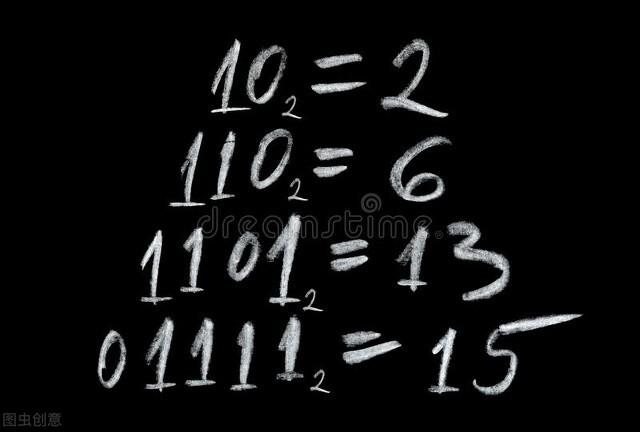我们先看几个小学时做过的题目,那时的数据较小,可以用列举法
问题1:图中有多少个不同的长方形?

问题2:能被72整除的正整数共有多少个?
问题3:现有2张1元纸币,3张5元纸币,从中拿出若干张(至少一张),可以组成多少种不同的币值?
首先这几个问题都可以用列举法,我们先试一试
问题1:答案是18个

问题2:答案是12个

问题3:答案是11种

好了,答案出来了,都是列举出来的,但是到了高中阶段,涉及到的数据就会大一些,可能结果会有好几十、好几百、甚至好几千,那想用列举法解题就不现实了
现在我们来学习将这些模型转化为分步乘法计数原理
针对问题1,目标是选出长方形,而长方形由两条横线和两条竖线组成,而题中有3条横线,4条竖线,分两步各选两条线后即可将长方形唯一确定下来

针对问题2,由于是约数问题,先将72进行质因数分解,72=2^3*3^2,仅有2,3这两个质因数,对于2而言,有2^0,2^1,2^2,2^3这4种选择,同理对3而言,有3^0,3^1,3^2这3种选择,共有4*3=12种

同样对于问题3而言,1元有0,1,2张3种可能,5元有0,1,2,3张4种可能,共12种,但是要减去1种,就是两个0的,因为至少一张,所以答案是11
显然通过转换成分步乘法计数原理之后,我们可以处理一些数据较大的情况了,比如
问题4:如图,含有字母“W”的长方形共有______个

问题5:能被300整除的正整数共有______个
问题6:小明有1张1元纸币,2张10元纸币,3张100元纸币,他从中取出若干张(至少一张),能组成______种不同的币值
同学们试一试,看学会了没?
下面公布答案

分别是48;18;23
如果你喜欢本文,请关注、点赞、转发、评论,谢谢你的支持!
,