一、定义法
根据等比数列的定义,判断
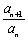
或

是一个与无关的常数.
例1 如果是等差数列,则数列
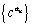
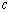
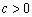
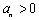
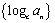

证明:若为等差数列,则有
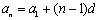
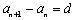

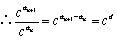
(常数),
故数列为等比数列.
同理,为等比数列,且时,
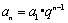

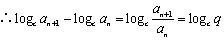
,
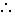
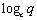
二、等比中项法
对于各项均不为零的数列,若对于任意大于1的正整数都有
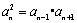
例2 已知
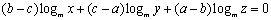
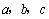
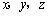
解:设等差数列的公差为
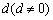
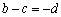
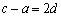
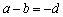
代入,
可得
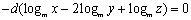

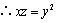
又
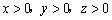
三、通项公式法
为等比数列
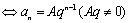
例3 已知是各项均为正数的等差数列,
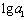
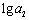
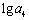

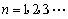
解:
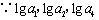
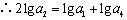
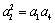
又设等差数列的公差为,
则
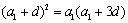
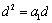
当
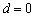
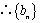
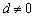

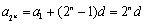
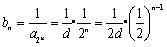
.
故是首项为
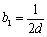
,公比为
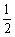
的等比数列.
四、递推公式法
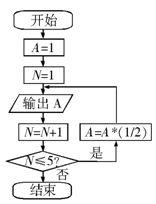
例4 根据如图所示的框图,写出所打印数列的前5项,并建立数列的递推公式.问:这个数列是等比数列吗?
分析:先求出前5项值,然后通过递推性质确定其通项公式.
解:若将打印出来的数依次记为

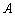

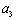

由图可知,

,

,

,
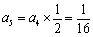
.
于是可得递推公式
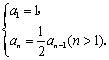
由于
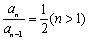
,因此这个数列是等比数列,
其通项公式是
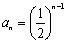
.
五、前项和公式法
在数列中,前项和为
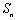
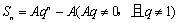
例5 已知数列的前项和为

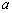
A.一定是等比数列
B.一定是等差数列
C.是等差数列或是等比数列
D.既不可能是等差数列,也不可能是等比数列
解:当
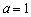
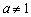
六、反例法
若判断一个数列不是等比数列,则反例法显得更简单.
例6 设,是公比不相等的两个等比数列,
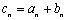
解:设,的公比分别为
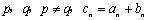
为证不是等比数列只需证
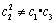
事实上,
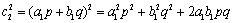
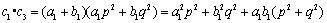
由于

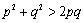
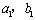
注意:有些试题常常需要由一个特别说明一个命题是错误的,但应当注意一个特例不能说明命题是正确的.