“ 割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。”
上次用scratch做练习,发现画正多边形,当边数特别大的时候看起来就很想一个圆。
“咦,这个怎么变成一个圆形了呢?” 看到这里,京京有点惊奇。
京京爸,公众号:平凡技术人生从正多边形到圆
今天打算和京京一起沿着正多边形,继续研究下π的秘密。
01
—
圆周率的历史

我们所学知识,大多都是古代先人从解决日常生活中问题总结得来的。推理来看,古人肯定先认识圆,而后才来研究圆,最终发现圆周率的奥秘。
《史记》中《夏本纪》有记录大禹治水中关于圆的描述:“左准绳,右规距”。用这里描述的规距,就能画出圆形。
而荀子也说:“木直中绳,輮以为轮,其曲中规。”。翻译过来就是说,笔直的木条,用火烧烤,使其弯曲成轮。这个时候,木条的弯度就很像一个圆了。
并且,古代时候,天空中同样也会有月亮,太阳,这些都会让人第一时间认识圆。而对圆的研究就比较靠后了。在人们不断发现、研究过程中,人们发现,圆周长和圆直径成正比例关系,并且这个数字恒定不变。
在人们追究这个数字到底等于多少的过程中,也开启了人们对于圆周率的研究。公元263年,我国古代有个叫刘徽数学家,他用一种割圆术的办法,来研究圆周率等于多少?

经过无数次的研究计算,刘徽给出圆周率等于:3.141024。
到了南北朝时期,我国古代著名的数学家祖冲之给出了,圆周率的更准确的近似值区间:3.1415926到3.1415927之间。而据说,祖冲之如何算出这个近似值到目前为止还是一个谜。
关于圆周率的研究,古今中外的科学家前仆后继的一波又一波。
1706年,英
国数学家威廉·琼斯,第一次用

来表
示圆周率。
到了1736年,瑞士大数学家欧拉也开始用

表示圆周率。从此,

便成了圆周率的代名词。
说到这里,我笑着给京京说,欧拉这个人,你要记清楚。未来很多年他都会陪着你学习成长。你清晰的认识他,就能学习很轻松。你不能深刻理解他,那他会是一个噩梦。O(∩_∩)O哈哈~

是一个无理数,小数点后有多少位,不得而知,目前计算到的小数点后数字有31.4万亿位。

02
—
自己动手计算π
如上面所说,可以通过圆内切正多边形近似等于圆周,那么π就等于多边形边长之和除以直径。其中n是正多边形的边数,r是正多边形的边长,d是直径。

我们用scratch可以构造一个积木程序,来计算这个

的值。
构思:
第一步,我们修改之前的画正多边形的积木,让其从(0,0)开始。
第二步,将角色运动的y坐标记录汇总。
第三步,在汇总数据中找到最大的y值,即可近似等于直径。
最后,根据公式计算出自己计算的圆周率值。
我们如何存储这个y坐标呢?scratch当中有一个列表的积木。

新建一个直径列表,scratch就会出现一堆积木:

而上图中红框里面的积木,就可以把直径记录下来。
好了,下来,我们画一个边长为6,的正80变形。
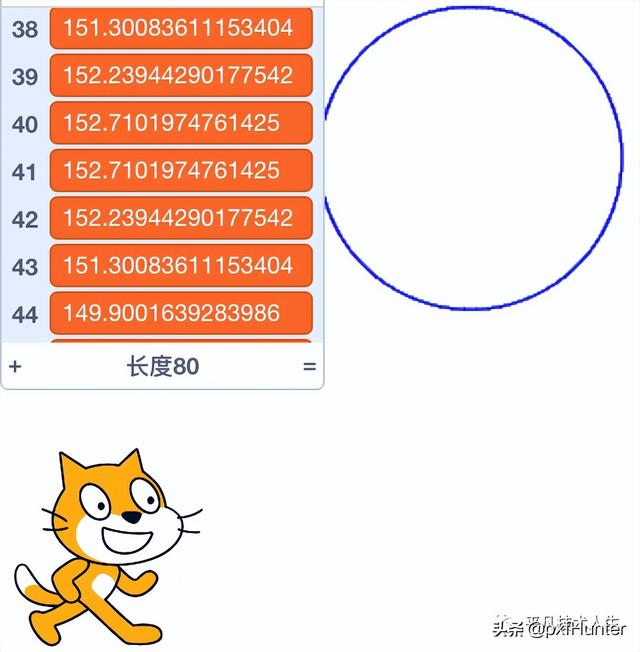

最后算得,π=3.14320857。
我们再把边长扩大下,看看结果,这次,我们画个正200边形,边长为1.1。

通过上面的公式继续计算可得:π=3.14185107。
看来确实正多边形边数越大,越能接近圆周率的近似值。这些内容,京京都还不明白。只能当做好玩的工具看看了。
与其说,我陪着京京研究动手实践下如何计算圆周率,倒不如说,通过scratch工具加深了我自己这么多年对圆周率的更深层次的认知。印象中,一直只是记得π=3.14。至于π的前世今生,不得而知。
之前也确实缺少一个比较直观的工具来模拟这个。现在通过scratch画图工具确实很清晰、明了的了解π的计算含义。

希望,京京在学到圆的知识的时候,能自己动手实践出自己计算的π值。
,




