一道高中立体几何题-求两点之间的最短距离
一个正四面体的顶点为A, B, C, D, 每个棱的长度都是1, 点P在棱AB上, 点Q在棱CD上, 求P和Q之间的最短距离。
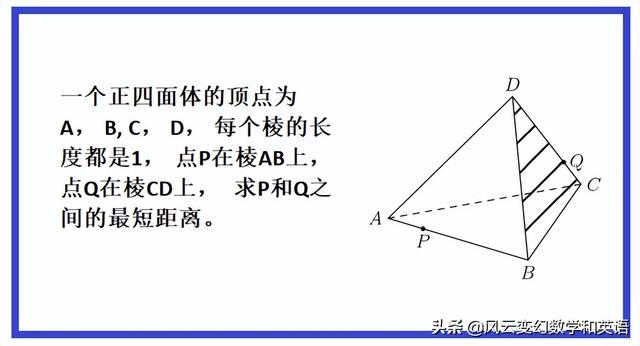
解法1:两点之间垂线最短, 这样PQ最短距离的出现, 应该是P是AB的中点, Q是DC的中点。

如上图,这样连接PC和PD, 可以知道PD=PC, 因为四个面都是全等的等边三角形, 其中线也相等。 因此PQ垂直于CD。
对于边长为1 的等边三角形,其中线PC=PD=(√3)/2, 而QC=1/2,
所以根据勾股定理, PQ的值:

解法2:如下图, 有点D做DD’垂直于底面, D’是垂足,连接CD’, 由于是正四面体, 所以D’是三角形ABC的中心, 所以CD’则是底边中心的2/3, 这是由中心的性质决定的。由此得知三角形DCD’是直角三角形。

可以算出:
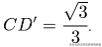
因为:

而:

根据余弦定理:
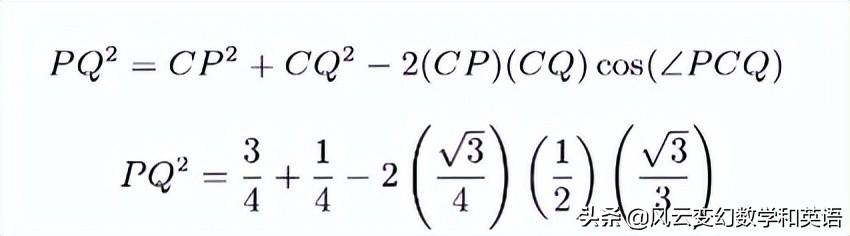
最后得出:






