很多人大概都听说过广义相对论是爱因斯坦描述引力的几何理论,也都听说过引力会导致时空弯曲这样的结论。但很多人并不清楚爱因斯坦是如何想到把引力这样一个纯粹的物理问题和几何这样一个纯粹的数学问题联系起来的。为了说清楚这点,我们还得从广义相对论的基本公理,即“等效原理”出发(注:广义相对论还有一条公理是所谓“广义协变原理”,它只是狭义相对性原理的自然推广,要求物理规律必须以张量方程的数学形式表述以保证其在任意坐标变换下协变,但这条公理将不作为本篇文章讨论的重点)。
等效原理告诉我们:引力和加速系等价。这件事情第一眼看上去很显然,但是这个原理真正的微妙之处在于:这里说的等价只是局部等价而不是全局等价!比如一个站在地球表面的人和一个处于理想的没有任何物质的外太空中做匀加速运动的人(假设加速运动的加速度和地球表面的引力加速度大小相等方向相反)无法“区分”自己到底处在哪种情况。注意:此处的“区分”加引号是因为这两种情况还是可以被区分的:站在地球表面的人如果仔细测量还是能发现离地面不同高度不同位置的身体的各个部位所受到的地球引力的大小和方向是存在很细微的不同的。离地面越高的部位受到的引力越小,反之越大。也就是身体上不同部位对应不同的引力加速度。所以这些不同的引力加速度是不能被一个单一的全局加速系取代的。
这种现象产生的根本原因在于宇宙中真实的引力场是由诸如行星,恒星等物质产生的。也就是说,引力场是有源的,它在数学上对应非零的散度!(这里更准确的说法不是源而是汇 - sink,因为不像电荷有正有负,由于质量恒正,引力场的力线总是终止于产生该引力场的物质上,所以是汇。)所以根据高斯定理可知,正是这种有源性导致宇宙中并不存在空间各处完全均匀的引力场。所以由它产生的真实的引力效应是无法被一个全局均匀的加速系替换掉的(注:真实的引力效应会对物体产生不可消除的切向挤压径向拉伸的可观测的形变效应,这种效应叫做“潮汐力”,潮汐力是表征引力最重要的特征)。所以等效原理严格来说只在空间无穷小(局部)的范围里才成立。

潮汐力示意
在上面的例子里,因为人的横向尺度和径向高度相对于地球半径来说都太小了,所以我们才可以近似地认为他身体的每个部位都受到大小和方向完全相同的引力,然后才能应用等效原理把它替换成一个单一的加速系。然而对于一个和地球尺度可比拟的物体来说,我们就不能对整个物体直接应用等效原理把它受到的来自地球的引力用一个单一的全局加速系替换掉。这时候我们只能把物体分成很多无穷小的局部区域,然后对每个局部区域逐个应用等效原理将其受到的引力等效替换成一堆局部加速系。所以整块物体受到的来自地球的引力就可以被等价成无穷多个局部加速系的拼接(严格的数学用语叫“联络”)。
所以到此为止,我们已经从等效原理出发,得出了引力 = 无穷多局部加速系的拼接这一极为重要的物理洞察!以上只是定性的推理,为了定量描述这些加速系,我们可以从最简单的非相对论性运动学出发(即不考虑狭义相对论对运动速度上限的限制以及不同参考系中的时间膨胀和长度收缩等效应)看看时空图里的加速系(加速运动)是如何表示的从而获得一些物理直觉。

不妨先从最平庸的加速度a=0做匀速直线运动的参考系开始考虑。假设初始位置是x=x,速度恒为v=v。所以相对于坐标原点处一个静止不动的观察者来说,这个匀速运动的参考系在某一时刻t的位置坐标是x(t)=x vt。所以我们可以反解出时间t和位置坐标x的函数关系是t(x)=(x-x)/v的线性形式。为直观起见,下面作出了这个表达式在不同初始位置下的函数图像(为了作图方便假设v=1m/s)。其中斜线代表了处在坐标原点静止不动的观察者看到的匀速运动参考系的时空轨迹,竖线代表了处于那个做匀速运动参考系上的观察者看到的这个参考系的时空轨迹。
容易发现,在不同的参考系下,这一系列横向等距平行的竖线(直线)被映射到一系列横向等距平行的斜线(仍然是直线!)。没有任何有趣的事情发生。
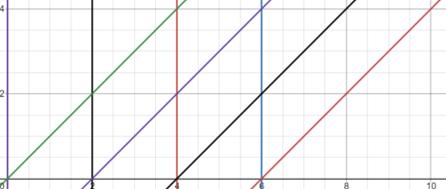
图1 –匀速系的时空图。纵坐标是时间,横坐标是位置
现在考虑稍微复杂一点的情形:一个参考系做一维匀加速直线运动(即一个全局的匀加速系),初始位置是x=x,初始速度是v=0,加速度是a=g。所以相对于坐标原点x=0处一个静止不动的观察者来说,这个加速参考系在某一时刻t的速度是v=gt,位置坐标是x(t)=x gt/2。所以我们可以反解出时间t和位置坐标x的函数关系是t(x)=±[2(x-x)/g]。为直观起见,下面作出了这个表达式在不同初始位置x下的函数图像(为了作图方便假设g=1m/s)。其中曲线代表了处在坐标原点静止不动的观察者看到的匀加速直线运动参考系的时空轨迹,竖线代表了处于那个做匀加速直线运动参考系上的观察者看到的这个参考系的时空轨迹。
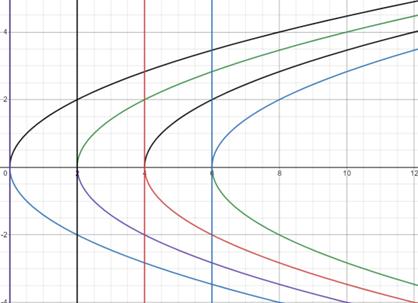
图2 –加速系的时空图。纵坐标是时间,横坐标是位置
容易发现,在不同的参考系下,这一系列横向等距平行的竖线(直线)被映射到一系列横向等距平行的曲线(注意这里是曲线!)。也就是说,在我们使用了加速系以后,原先平直的时空坐标系变成了弯曲的时空坐标系。然后应用等效原理,即加速系和引力等价,我们可以得出“引力”和全局等加速度弯曲的时空坐标系等价!也就是说,我们现在可以把这个全局的加速系a=g替换成一个全空间均匀的“引力场”,这个“引力场”在每点的强度都是a'=-g,沿x轴负方向。注意:此处的“引力场”加引号是因为此处的所谓“引力场”是虚假的,我们可以通过一个简单的坐标变换x'=x-gt/2把这个“引力”在全空间彻底消除!
所以这里所谓的“引力效应”并不是真实的由物质产生的广义相对论希望描述的引力,而仅仅是因为我们使用了不好的坐标系所导致的!一旦我们换到了好的坐标系,这些虚假的“引力”就会立刻消失!然而,说这个物理图景不能描述真实的引力并不意味着它就完全没价值需要被彻底放弃。注意我们之前说的是:引力 = 无穷多局部加速系的拼接,我们并没直接说引力 = 加速系。所以无穷个局部加速系的拼接应该对应于无穷个局部等加速度弯曲(但全局不等加速度弯曲)的时空曲线坐标系的拼接,也就是对应于一个每点加速度都不一样的弯曲时空坐标系。然后真实的引力效应就应该被解释成:如果对一块区域施以任何的坐标变换都无法把原先弯曲的时空坐标系全局地变成平直坐标系的形式(注:这里的平直坐标系指的不是欧几里得空间里由克罗内克delta度规定义的平直坐标系而是狭义相对论里由闵可夫斯基度规定义的平直坐标系以满足光速不变原理),那么在这块区域里就一定存在真实的无法被消除的由物质产生的引力。

质量引起时空弯曲
也就是说,真实的引力是时空坐标系所描述的时空的一种内禀属性。这种内禀属性是不会因为人为的坐标系的选取而被全局消除的。再联系到文章开头时说的“真实的引力效应会对物体产生不可消除的切向挤压径向拉伸的可观测的形变效应,这种效应叫做潮汐力”。所以潮汐力其实就是我们这里讲的时空的内禀属性对应的物理可观测量,是无法通过坐标变换移除的。说到这里,你应该会联想到19世纪黎曼等数学家发展出的黎曼几何里一个完全平行的数学类比,即曲面的黎曼曲率这种内禀属性是没法通过任何坐标变换移除的!
所以如果我们作如下的解释,即把物理里的时空解释成数学里的曲面(即一个抽象的弯曲空间/流形),把物理里观察者测得的具体的时空坐标/参考系和它们之间的变换解释成数学里抽象的坐标系和坐标系间的非线性变换,把物理里的潮汐力(真实的引力效应)解释成数学里的黎曼曲率,那么引力这样一个纯粹的物理问题就可以被等价地转化成黎曼几何这样一个纯粹的数学问题!这样我们就可以套用19世纪数学家们已经发展好的数学工具去解决物理上的引力问题。至此,我们已经从等效原理这一基本公理出发阐述了广义相对论核心的物理思想。

数学家黎曼
历史上,在得到等效原理并理清这里面重要的物理思想以后,爱因斯坦最先将他的等效原理应用到引力场对光线传播(或更一般的电磁现象)的影响。“把等效原理应用于像光这样的电磁现象(而不是力学现象)”是当时除了爱因斯坦没人想过的在思想上革命性的飞跃!下面我们就定性半定量以一种不严格的手法在牛顿力学的框架下应用等效原理讨论一下光线掠过太阳表面时的偏转并给出该偏转角度一个大致的估计(虽然定量上是错的,但已经能给出足够深刻的物理洞察)。尽管我们现在还没给出严格的广义相对论的场方程,但是仅仅依据等效原理这一强有力的公理,我们就已经能够推断出:太阳表面对光的引力作用可以被等价成光处在一个与太阳表面所产生的引力加速度大小相等方向相反的加速系里,而在这个加速系里光走的路径会发生弯曲!(这里可以把加速系想象成是一个加速电梯)。所以我们这里仅仅依据这一条看似平凡的等效原理就已经定性地预言了光在引力场下的传播轨迹会发生弯曲这一非平凡的结论!
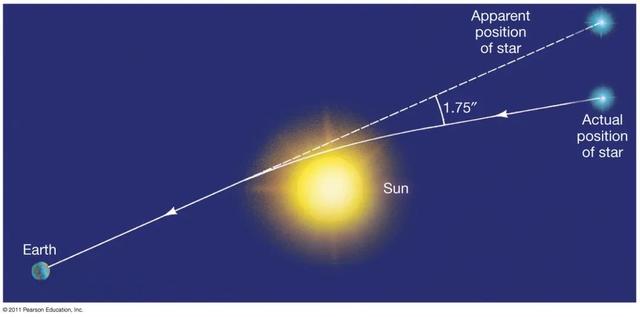
光线在太阳引力场中弯曲 | 来源
假定太阳引力场的有效作用范围就在它的一个直径范围内,则这个假想的加速电梯的宽度将刚好横跨一个太阳直径2R的范围。根据上述等效原理给出的推断可以得出:太阳表面产生的引力效应可以被等价替换一个电梯t=0在时刻从静止在太阳表面的位置开始沿径向垂直远离太阳表面的方向做匀加速直线运动,加速度的大小g等于太阳表面的引力加速度的大小,方向与其相反,即:
假设一束光在t=0时刻从电梯的最左端水平向右射出。光的水平运动可以用匀速直线运动(水平速度用光速c做个估计)做个大致的估算,所以光从电梯最左端到达最右端所需要的时间大致是:
由于光在竖直方向的初始速度是0,加速度近似是g竖直向下指向太阳中心,所以我们可以大致估算出Δt时间后光抵达电梯最右端时速度的竖直向下的分量是:
所以我们得出光线抵达电梯最右端时的偏转角估计值(等价于光线掠过太阳表面时的偏转角)是:
因为上式分子中的万有引力常数G很小,而分母中的太阳半径R和光速的平方c很大,所以光线掠过太阳表面时的偏转角非常非常小难以观测!
所以这里我们已经通过一些不严格的定性半定量的计算在牛顿力学的框架下从等效原理出发给出了光线偏转角的估计值和大致的数量级。这个结果给出了很多关键的物理图像和信息!而且更令人惊讶的是,这个如此容易计算的估计值竟然和用复杂的广义相对论场方程严格计算出来的精确值之间仅相差一个系数2!
【注:下面这个偏转角就是用场方程严格计算出的结果,即真实的偏转角是估计值的2倍】
未编号的图片为编辑者配图,来源于网络
编辑:云开叶落
,